Có rất nhiều bài toán thực tế mà việc giải nó lại quy về việc tìm giá trị lớn nhất, giá trị nhỏ nhất của một hàm số nào đó. Loạt bài viết này Thapsang.vn sẽ giới thiệu một số bài toán như thế và tập trung vào việc phân tích bài toán từ đó rút ra quy trình chung để giải chúng.
LƯU Ý:
* Có nhiều cách để tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số và đạo hàm là công cụ mà chúng ta sử dụng ở đây. Vì thế loạt bài viết phù hợp với các bạn đã và đang học lớp 12, sinh viên, giáo sinh và giáo viên sư phạm toán.
* Đây là bài viết đầu tiên với đối tượng chính là các bạn học sinh lớp 12 và lần đầu gặp bài toán dạng này, tuy nhiên với các bạn đã từng giải dạng toán này vẫn có thể đọc để biết thêm các khía cạnh khác, còn với các bạn chưa học đạo hàm thì hãy bỏ qua phần 3 của bài viết.
* Các bạn học sinh không cần đọc các chú thích có chữ GV, chúng được tác giả dùng để trao đổi riêng với các bạn đồng nghiệp.
Sau đây chúng ta xét một bài toán thuộc loại khá phổ biến, trích từ đề thi Giữa HK1 năm học 2016-2017 của trường THPT Nguyễn Du – Nam Định.
1. Bài toán thực tế
nước, có dạng hình hộp chữ nhật với đáy là hình vuông và không có nắp. Hỏi chiều dài, chiều rộng và chiều cao của lòng bể bằng bao nhiêu để số viên gạch dùng xây bể là ít nhất? Biết thành bể và đáy bể đều được xây bằng gạch, độ dày của thành bể và đáy là như nhau, các viên gạch có kích thước như nhau và số viên gạch trên một đơn vị diện tích là bằng nhau.
Hình chụp đề thi Giữa HK1 năm học 2016-2017, trường THPT Nguyễn Du – Nam Định
2. Phân tích
Toán học hóa
* Nhận xét rằng, vì “độ dày của thành bể và đáy là như nhau, các viên gạch có kích thước như nhau và số viên gạch trên một đơn vị diện tích là bằng nhau” nên số viên gạch cần dùng để xây sẽ ít nhất khi và chỉ khi tổng diện tích bề mặt các thành và đáy của lòng bể là nhỏ nhất.
* Bài toán giờ trở thành tìm kích thước của hình hộp chữ nhật để tổng diện tích của mặt đáy và 4 mặt xung quanh là nhỏ nhất. Mà “cần tìm gì thì gọi đấy”1 thôi 😀
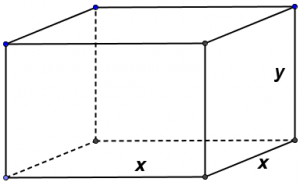
Cần tìm gì thì gọi đấy 🙂
Vì thế nếu gọi 
lần lượt là chiều dài, chiều rộng và chiều cao của lòng bể và 
là tổng diện tích bề mặt của lòng bể thì ta có: 
với 
Vấn đề
* Tiếp theo chúng ta cần làm gì? Đó là tìm 
để nhỏ nhất. Đây thật sự là một vấn đề2, vì sao? Vì từ trước tới giờ chúng ta chỉ có các quy tắc, phương pháp cho bài toán tìm giá trị nhỏ nhất của những biểu thức chứa 1 biến mà thôi3, trong khi lại là biểu thức chứa 2 biến và chúng ta chưa có sẵn công thức, định lý, quy tắc hay phương pháp nào cho bài toán 2 biến như thế cả. Vậy thì phải làm thế nào?
* Hãy bình tĩnh và cố gắng phát biểu vấn đề một cách rõ ràng, rồi nhớ lại xem trong những tình huống tương tự như vậy thì chúng ta thường tư duy như thế nào?
Vấn đề: Đã biết cách tìm giá trị nhỏ nhất của biểu thức 1 biến và cần tìm giá trị nhỏ nhất của biểu thức 2 biến.
Điều này có nghĩa là gì? Chúng ta có một câu hỏi cũ, “tìm giá trị nhỏ nhất của một biểu thức”, nhưng cần trả lời trong 1 điều kiện mới là biểu thức đó chứa 2 biến. OK? Chính xác là như thế. 🙂 Trong những tình huống như vậy, lời khuyên mà các “sư phụ” của chúng ta thường đưa ra là gì? 🙂
Phương pháp tư duy
* Lời khuyên đó là: Quy bài toán chưa biết giải về bài toán đã biết giải hay còn gọi là “quy lạ về quen”4. Cụ thể ở đây, nếu ta có thể đưa biểu thức , từ biểu thức phụ thuộc 2 biến, trở thành biểu thức phụ thuộc vào 1 biến thì bài toán được quy về bài toán quen thuộc. Nhưng điều này chỉ xảy ra khi hai biến 
và 
phải có một quan hệ nào đó. Vậy hai biến này có quan hệ gì không?
* Hãy quay lại đề bài của bài toán, có 1 giả thiết mà chúng ta chưa dùng tới. Thật vậy, theo giả thiết thì thể tích của bể là nên ta có phương trình 
và đây chính là điều chúng ta cần, một phương trình quan hệ giữa và .
* Từ (2) ta có thể rút được biến này theo biến kia và thế vào (1), khi đó chỉ phụ thuộc vào 1 biến, đó chính là mục tiêu của chúng ta. Nhưng chúng ta sẽ rút biến nào theo theo biến nào, theo hay theo và tại sao?
Chắc bạn đang lẩm bẩm “Sao ông này kì zậy, hiển nhiên là rút theo rồi, rõ như ban ngày vậy còn hỏi lí do làm chi? Phức tạp hóa vấn đề quá haizz.” 😀 Ờ, đúng thế, quá hiển nhiên, nhưng mà rõ như ban ngày thì mới khó giải thích chứ tối như ban đêm thì giải thích làm gììì. 😀 Chém gió thế đủ rồi, tóm lại là “mình thích thì mình rút thôi” 😀 .
Ta có 
, thay vào (1) được 
và bài toán giờ chỉ còn là tìm 
để hàm số đạt giá trị nhỏ nhất, một bài toán toán học quen thuộc.
3. Tìm giá trị nhỏ nhất của hàm số
Bài toán: Tìm để hàm số sau đạt giá trị nhỏ nhất với x > 0.
Việc giải bài toán này với các bạn học sinh lớp 12 thì dễ dàng thôi, còn với các bạn chưa học đạo hàm thì có thể vất vả hơn chút.
* Ta có 
và 
* Bảng biến thiên
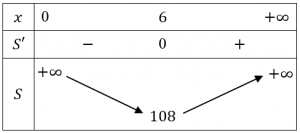
* Do đó hàm số đạt giá trị nhỏ nhất khi 
.
4. Đáp số
Với suy ra 
nên chiều dài, chiều rộng và chiều cao cần tìm là 
.
5. Quy trình chung
Qua phân tích trên, chúng ta có thể rút ra một quy trình chung để giải quyết các bài toán thực tế mang tính tối ưu như trên theo các bước sau:
Bước 1: Toán học hóa bài toán.
* Thực chất là đại số hóa, gọi các đại lượng cần tìm và đã cho trong bài toán.
* Từ điều kiện của bài toán thiết lập được 1 hàm số phụ thuộc vào 1 biến.
Bước 2: Tìm giá trị lớn nhất hoặc giá trị nhỏ nhất của hàm số trên, tùy theo yêu cầu của bài toán
Chúng ta thường dùng công cụ đạo hàm ở bước này, mặc dù có thể sử dụng công cụ khác nhưng có thể khó khăn hơn.
Bước 3: Kết luận bài toán ban đầu
Trong thực tế có rất nhiều bài toán tương tự như bài toán trên, dưới đây là một vài ví dụ.
6. Bài toán tương tự
Bài 1. Một xưởng cơ khí nhận làm những chiếc thùng phi với thể tích là 
. Hỏi mỗi thùng phải có kích thước thế nào để vật liệu làm là ít nhất.5
Bài 2. Bạn muốn xây dựng một bể chứa nước hình trụ có thể tích 
. Đáy bể làm bằng bê-tông giá 100 ngàn đồng trên 
, thành làm bằng tôn giá 90 ngàn đồng trên , nắp bằng nhôm không gỉ giá 120 ngàn đồng trên . Hỏi kích thước của bể phải như thế nào để chi phí xây dựng là nhỏ nhất?6
Bài 3. Công ty Vinamilk có hai dòng sản phẩm sữa tươi với bao bì là hộp giấy, loại 
và loại 
. Để sản xuất bao bì hộp giấy cho hai loại đó, công ty Vinamilk đã đặt hàng hai công ty khác, một là Combibloc ở Đức và một là Tetra Pak ở Thụy Điển. Hai công ty này đã thiết kế các hộp có kiểu dáng và kích thước khác nhau như hình ảnh dưới đây.
Ảnh: Internet
a) Công ty nào đã sử dụng ít nguyên vật liệu hơn với từng loại hộp và ?
b) Giá sản phẩm của công ty nào rẻ hơn?
7. Bình luận
* Dựa trên câu hỏi mấu chốt là “số viên gạch ít nhất”, bài toán trên có thể phát biểu theo nhiều cách khác. Chẳng hạn, nếu biết độ dày của thành bể, đáy bể, kích thước của mỗi viên gạch và giá thành của gạch thì câu hỏi của bài toán có thể trở thành “Kích thước của bể là như thế nào để số tiền mua gạch là ít nhất”?
* Học đi đôi với hành, lý thuyết gắn liền vơi thực tế là những nguyên lý giáo dục cơ bản và có nhiều tín hiệu đáng mừng là chúng được thể hiện khá rõ trong đề thi minh họa Kỳ thi THPT Quốc gia 2017 của Bộ Giáo dục và đào tạo gần đây.
* Thực tế dạy và học thì những bài toán mang tính thực tiễn như trên có thể xuất hiện rất sớm trong chương trình toán, chứ không phải đợi đến lớp 12. Chẳng hạn, ngay từ lớp 10, thậm chí là lớp 9 thì học sinh có thể giải được những bài toán thực tế vui vui như dưới đây, mời bạn thử sức. 😀
Câu chuyện giữa hai người yêu toán, Bá và Chí. Họ có một hợp đồng lao động là Chí làm công cho nhà Bá 10 năm và tiền công được thanh toán theo 5 năm một lần, nhưng vì cả hai đều là người yêu toán nên cách thanh toán tiền công của họ cũng đầy màu sắc toán học. 😎
Lần thứ nhất: Bá trả công cho Chí
Sau 5 năm đầu làm công ở nhà Bá, Bá trả công cho Chí một miếng đất trên ruộng của Bá bằng cách đưa cho Chí một sợi dây dài 40m và bảo Chí dùng sợi dây đó khoanh một miếng đất hình chữ nhật, miếng đất khoanh được là của Chí. Vấn đề của Chí là cần khoanh hình chữ nhật có kích thước như thế nào để miếng đất có diện tích là lớn nhất? 😀
Lần thứ hai: Chí “trả thù” Bá 😆
Năm năm sau, cũng sợi dây 40m ấy, Chí cầm đến nhà Bá đòi tiền công bằng cách yêu cầu Bá cắt cho Chí 2 miếng đất trên ruộng nhà Bá để Chí … đào ao 😛 . Một miếng hình vuông còn miếng kia hình tam giác đều và hai miếng phải dời nhau sao cho tổng chu vi của cả hai miếng bằng đúng chiều dài của sợi dây. Giờ Bá cần chia sợi dây đó làm 2 đoạn, mỗi đoạn dài bao nhiêu để tổng diện tích của 2 miếng đất là nhỏ nhất? 😀
Theo bạn thì giữa Bá với Chí, ai “hiểm” hơn ai? 😈
Nếu bạn biết một bài toán thực tế nào khác hoặc có ý kiến về bài viết, xin hãy chia sẻ và gõ nó vào hộp bình luận phía dưới nhé. Cảm ơn bạn!
Hết phần 1, cảm ơn bạn đã đọc bài viết, mời bạn đón đọc phần 2.
- Xem thêm bài Khẩu quyết trong toán học [↩]
- GV: Theo lý luận phương pháp dạy học môn toán thì đây là một tình huống có vấn đề [↩]
- Đặc biệt, học sinh lớp 12 được học tường minh phương pháp tìm giá trị lớn, giá trị nhỏ nhất của các hàm số 1 biến bằng công cụ đạo hàm [↩]
- GV: Trong phương pháp dạy học và giải quyết vấn đề thì “Quy lạ về quen” là một kĩ thuật tư duy được áp dụng trong bước giải quyết vấn đề và thường được sử dụng trong tình huống gặp một câu hỏi quen thuộc nhưng ở những điều kiện mới. [↩]
- Tham khảo từ một tài liệu trên Internet, không rõ tác giả [↩]
- Tham khảo từ một tài liệu trên Internet, không rõ tác giả [↩]
Để lại một bình luận