“Nhánh vô cực nhưng bị cụt” – đó là một trong các lỗi hay gặp ở các học sinh lớp 12 khi mới học về chủ đề “Khảo sát sự biến thiên và vẽ đồ thị của hàm số bậc ba”. Tại sao lại có hiện tượng này, nguyên do từ đâu, có cách nào giúp học sinh không tái lỗi này? Bài viết chia sẻ một vài kinh nghiệm thực tế.
1. Hiện tượng này như thế nào?
Hiện tượng này thường xảy ra khi học sinh mới làm quen với bài toán vẽ đồ thị của hàm số bậc ba. Chẳng hạn, khi giải bài toán “Khảo sát sự biến thiên và vẽ đồ thị của hàm số 
”, một học sinh đã vẽ đồ thị của hàm số đó như hình dưới đây:
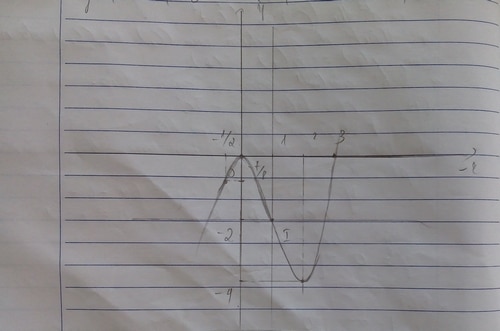
Đồ thị mà học sinh đã vẽ có gì đặc biệt? Với đề bài như vậy, là giáo viên, chắc bạn sẽ nhận ra ngay vấn đề, đúng vậy, một nhánh vô cực của đồ thị đã bị “cụt ngủn”, nó chưa vượt qua điểm cực tiểu của đồ thị.
2. Nguyên tắc vẽ nhánh vô cực
Chắc hẳn lời giải của học sinh này khiến bạn có một chút không vui, vì khi giảng ở tiết lý thuyết bạn đã lưu ý, thậm chí là nhấn mạnh, học sinh rằng: “Nhớ vẽ nhánh vô cực kéo dài qua điểm cực trị (nếu có) của đồ thị một chút”. Và bạn cũng đã giải thích cơ sở của việc vẽ như vậy.
Về nguyên tắc, lý thuyết, khi 
dần tới âm vô cực thì nhánh vô cực tương ứng của đồ thị hàm số trên sẽ tiến dần tới âm vô cực. Tức nó sẽ “vượt quá” điểm cực tiểu kia của đồ thị rất nhiều. Trong thực hành, chúng ta “chấp nhận” mức độ tối thiểu là vẽ phải các nhánh vô cực vượt quá điểm cực trị (nếu có) của đồ thị hàm số là được. Chứ lấy đâu ra giấy mà vẽ tới “vô cực”. 😀
Nhưng tại sao học sinh vẫn mắc lỗi? Dù bạn đã giải thích rõ cơ sở của nguyên tắc vẽ như vậy.
3. Nguyên nhân
Nguyên nhân có thể là do học sinh “lơ đãng” không nghe giáo viên lưu ý, cũng có thể là nghe nhưng quên, cũng có thể là biết nhưng ẩu thả,… Nhưng thực tế giảng dạy cho thấy, dù bạn có nhắc lại khi học sinh quên thì tình huống vẫn có thể lặp lại sau một thời gian nào đó. Vậy nguyên nhân sâu xa, thực sự của hiện tượng này là gì? Tác giả cho rằng, nó nằm ở việc học sinh không nhận thức được tầm quan trọng của việc vẽ đúng “nguyên tắc”.
4. Biện pháp
Làm thế nào để học sinh không tái lỗi này? Ngoài việc làm mẫu chuẩn xác, lưu ý và nhấn mạnh khi dạy vẽ thì giáo viên nên làm cho học sinh thấy được, đâu là hình vẽ đúng nguyên tắc, là chuẩn và đâu là sai. Hậu quả sẽ ra sao nếu vẽ sai?
a) Hình vẽ đúng, hình vẽ sai
Chẳng hạn, trong tình huống trên, chúng ta có thể cho học sinh quan sát hình ảnh sau:
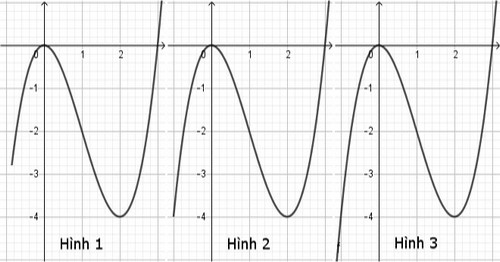
Và đặt câu hỏi “Căn cứ vào giới hạn của hàm số khi dần tới âm vô cực thì hình vẽ nào đúng? Tại sao?” Học sinh sẽ dễ dàng nhận ra đồ thị của hình 1 và hình 2 là sai còn hình 3 là chính xác.
b) Hậu quả nếu vẽ sai
Tuy nhiên, biện pháp trên mới chỉ dừng ở mức làm học sinh “Hiểu thế nào là vẽ đúng, vẽ sai”. Để học sinh nhận thức sâu sắc hơn tầm quan trọng của việc phải vẽ đúng, giáo viên cần thiết kế ra những tình huống mà “Nếu học sinh vẽ sai, đáp số của bài toán sẽ sai”. Nói rộng hơn “Nếu anh làm sai, anh sẽ lãnh hậu quả”. (Có vẻ hơi nghiêm trọng 😀 )
Chẳng hạn, cho học sinh phân tích tình huống sau:
Chuyện gì sẽ xảy ra nếu một bạn vẽ đồ thị của hàm số
để phương trình
có nghiệm duy nhất.”.
Qua đó học sinh sẽ nhận thức sâu sắc hơn tầm quan trọng của việc vẽ đúng nhánh vô cực, là phải “vẽ quá điểm cực trị (nếu có)”.
5. Bình luận
* Mặc dù việc giảng dạy chủ đề khảo sát và vẽ đồ thị của hàm số trong trường phổ thông giờ đây không còn quá chú trọng kỹ năng vẽ đồ thị của hàm số. Tuy nhiên, việc tìm hiểu, phân tích và sửa chữa các sai lầm về kỹ năng vẽ đồ thị cho học sinh không chỉ đem lại giá trị về kiến thức, kỹ năng mà còn là những bài học mang tính giáo dục về thái độ làm việc và học tập.
* Những sai lầm như tình huống trên suy cho cùng đều bắt nguồn từ thái độ không “tuân thủ nguyên tắc, quy luật”. Thái độ – một trong các mục tiêu mà người học phải nỗ lực để đạt được trong bất cứ bài học, giờ học nào và ở góc độ nào đó mục tiêu này còn quan trọng hơn cả mục tiêu kiến thức, kỹ năng. Kiến thức, kỹ năng cho bạn hiểu biết và hoàn thành công việc. Thái độ cho bạn thành công.
* Nếu bạn có những biện pháp khác hay ý kiến khác về bài viết, xin hãy chia sẻ nó vào hộp bình luận phía dưới. Cảm ơn bạn!
| “ | "Thái độ làm việc mới là yếu tố tiên quyết dẫn tới thành công trong công việc chứ không phải là mức độ thông minh." | ” |
|
— Carol Dweck (Đại học Stanford) |
Để lại một bình luận