Khi nhìn các hình chóp trong SGK, bạn có thắc mắc tại sao người ta thường vẽ đường cao của hình chóp theo phương thẳng đứng? Không chỉ SGK, các thầy giáo/cô giáo cũng thường vẽ như thế. Có cơ sở nào không cho việc vẽ như vậy?
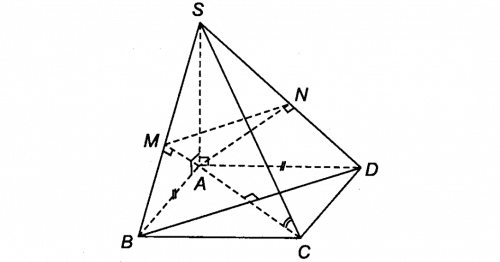
Hình chóp S.ABCD có SA vuông góc với đáy1
Tác giả chưa từng thấy ai, tài liệu nào, lý giải về vấn đề này. Bài viết này tác giả đưa ra kiến giải của mình từ đó rút ra một vài kết quả cho việc dạy và học. Theo tác giả có cả cơ sở lý thuyết và cơ sở thực tế cho việc vẽ như thế.
1. Cơ sở lý thuyết
Chúng ta biết rằng đường cao của hình chóp là đoạn thẳng nối đỉnh của nó với hình chiếu vuông góc của đỉnh trên mặt đáy2, hiển nhiên đường cao luôn vuông góc với mặt đáy. Mặt khác, có duy nhất một đường thẳng đi qua một điểm cho trước và vuông góc với một mặt phẳng cho trước.3
Như vậy, trong vô số các đoạn thẳng kẻ từ đỉnh của hình chóp tới mặt đáy thì chỉ có 1 và chỉ 1 đoạn thẳng vuông góc với mặt đáy mà thôi và đó chính là đường cao.
2. Cơ sở thực tế
Thực tế, khi dựng một đoạn thẳng nối một điểm nằm ngoài mặt phẳng tới mặt phẳng này thì đoạn thẳng đó chỉ có thể rơi vào 1 trong 2 trường hợp: hoặc “nghiêng nghiêng” so với mặt đáy, hoặc “thẳng đứng” so với mặt đáy. Hơn nữa, trong vố số đoạn thẳng đó, chỉ có 1 đoạn thẳng “thẳng đứng” so với mặt đáy.
Trên cơ sở lý thuyết và thực tế đó, chúng ta xét tình huống sau đây.
3. Tình huống cơ bản
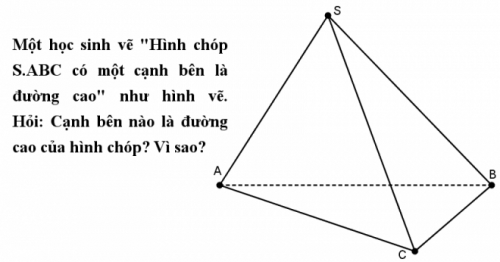
Tình huống: “Anh/chị hãy vẽ một hình chóp S.ABC, có một cạnh bên là đường cao của hình chóp và cho biết trong hình vẽ đó thì cạnh bên nào là đường cao của hình chóp?”
Theo cơ sở thực tế đã nói trên, hình vẽ của hình chóp S.ABC chỉ có thể rơi vào 1 trong 2 trường hợp sau: Hoặc cả 3 cạnh bên đều “nghiêng nghiêng” so với đáy; hoặc có 2 cạnh “nghiêng nghiêng” và cạnh còn lại “thẳng đứng” so với đáy. Cụ thể:
Trường hợp 1: Cả 3 cạnh bên đều “nghiêng nghiêng” so với đáy
Cả 3 cạnh bên đều “nghiêng nghiêng” so với đáy
Theo bạn, ở hình vẽ này thì cạnh bên nào là đường cao của hình chóp?
Chắc hẳn bạn sẽ trả lời “Cạnh nào chả được”. Đúng vậy, câu trả lời có thể là SA, cũng có thể SB hoặc cũng có thể là SC. Nhưng như thế là có vấn đề đấy! 😀 Tại sao lại vậy?
Trước tiên, cần khẳng định với hình vẽ như vậy thì cả 3 cạnh bên SA, SB và SC đều “nghiêng nghiêng” so với đáy, nói cách khác chúng có vai trò “ngang nhau/như nhau” so với đáy.
Khi đó, xét trường hợp SA làm ví dụ. Về lý thuyết, cho dù SA có hơi “nghiêng nghiêng/xiên xiên” so với đáy thì vẫn có thể chấp nhận SA là đường cao vì chúng ta biết rằng hình biểu diễn của một góc trong không gian không bảo toàn độ lớn của góc.
Nhưng nếu chấp nhận SA là đường cao thì dẫn đến việc cũng phải chấp nhận SB, SC là đường cao. Thật vậy, vì SB và SC cũng “nghiêng nghiêng/xiên xiên” so với đáy như SA, nên sẽ là không công bằng nếu “anh” nghiêng nghiêng thì được xem là đường cao còn “chúng tôi” cũng nghiêng nghiêng thì lại không? 😀
Tình huống thật nan giải, đường cao thì chỉ có một4 mà “anh” nào cũng đòi là đường cao. Phải làm sao đây?
Trong khi đó, anh “đường cao thật” than thở: Chỉ có mỗi tui là đường cao, chỉ có mỗi tui là vuông góc với đáy, những anh còn lại đều không vuông góc với đáy. Cớ sao lại vẽ tui cũng nghiêng nghiêng /xiên xiên như những anh kia. Vẽ như thế thì còn ai nhận ra tui nữa chứ! (“Em là ai giữa cuộc đời này”) 😀
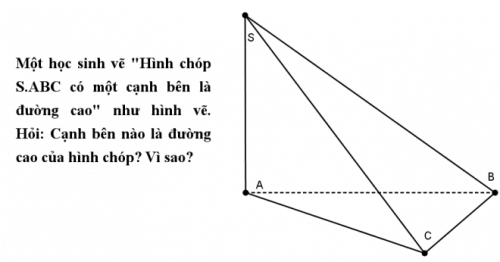
Trường hợp 2: Có 2 cạnh “nghiêng nghiêng” và cạnh còn lại thẳng đứng so với đáy.
Có 2 cạnh “nghiêng nghiêng” và cạnh còn lại thẳng đứng so với đáy
Theo bạn, ở hình vẽ này thì cạnh bên nào là đường cao của hình chóp?
Lập luận như trường hợp 1 ở trên, trong trường hợp này cả SB và SC đều “nghiêng nghiêng” so với mặt đáy nên cả 2 cạnh đều không là đường cao của hình chóp được. Do đó, cạnh bên còn lại, cạnh bên “thẳng đứng” so với đáy, là đường cao.
Ngoài ra, trong trường hợp này chúng ta có thể khai thác tính chất “Đường cao là đoạn thẳng ngắn nhất kẻ từ đỉnh tới mặt đáy” để chỉ ra đường cao. Tuy nhiên, tính chất này không áp dụng được cho trường hợp 1.
4. Kết luận
Ở tình huống trên, chúng ta chỉ xem xét việc vẽ đường cao là cạnh bên của một hình chóp tam giác và hiển nhiên, nó cũng đúng với các loại hình chóp còn lại như chóp tứ giác, chóp ngũ giác,… và cũng đúng với cả trường hợp đường cao không phải là cạnh bên.5
Tóm lại, khi làm việc với một bài toán về hình chóp mà đường cao của nó đã xác định và phải vẽ hình thì chúng ta nên vẽ đường cao của hình chóp đó theo phương thẳng đứng.
5. Dạy và học cách vẽ đường cao của hình chóp
Trong giảng dạy, kinh nghiệm cho thấy sau khi học sinh biết cơ sở lý thuyết nói trên thì nên định hướng ngay cho học sinh cách vẽ “đường cao” của hình chóp. Nếu không định hướng ở giai đoạn này, để học sinh vẽ tự do thì sau này sửa rất mệt.
Còn nếu gặp học sinh vẽ như trường hợp 1 thì chỉ cần đặt một câu hỏi là học sinh sẽ lúng túng và nhận ra sự bất hợp lý của hình vẽ, từ đó rút ra bài học là nên vẽ đường cao theo phương thẳng đứng. Câu hỏi gì vậy?
Đó là: “Trong hình vẽ của em, cạnh bên nào là đường cao? Tại sao không phải là một trong các cạnh bên còn lại?”
Chắc chắn học sinh sẽ lúng túng. Bạn thử xem! 🙂
Nếu bạn có một kiến giải khác hay bất kỳ ý kiến nào, xin hãy chia sẻ nó vào hộp bình luận phía dưới. Cảm ơn bạn!
Thực tế có không ít người luôn vẽ đường cao theo phương thẳng đứng, nhưng lại không/chưa lý giải được tường tận tại sao phải vẽ như vậy. Mình cũng từng như thế.
| “ | "Cái gì ta chưa hiểu tường tận thì chưa thuộc về ta." "What is not fully understood is not possessed." |
” |
|
— Johann Wolfgang von Goethe |
Để lại một bình luận