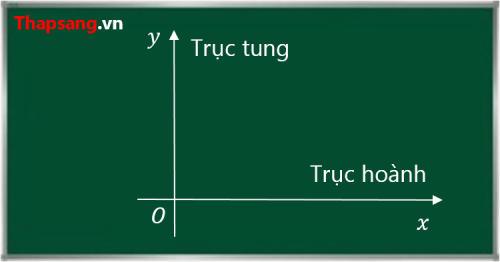
Bạn biết rằng “Hệ tọa độ Oxy gồm 2 trục, trục dọc gọi là trục tung, trục nằm ngang gọi là trục hoành …” và chắc rằng đã rất rất nhiều lần bạn vẽ hai trục đó. Nhưng bạn có bao giờ thắc mắc “tung” là gì, “hoành” là gì? Nếu chưa thì bạn giống mình rồi đấy!
1. Tung là dọc, hoành là ngang
Kể cũng lạ, học toán, làm toán và dạy toán bao năm nay, số lần vẽ hệ trục tọa độ, vẽ trục tung, vẽ trục hoành có lẽ lên đến hàng trăm lần. Nhưng gần đây mình mới biết ý nghĩa của hai từ tung và hoành: “Tung là dọc, hoành là ngang” và vì lẽ đó mà người ta mới gọi “Trục dọc là trục tung, trục ngang là trục hoành”.
Điều thú vị, khiến bài viết này ra đời là ở cái sự mình “phát hiện” ra ý nghĩa của 2 từ tung và hoành, thú vị ở chỗ mình hiểu ý nghĩa của hai từ này không phải do đọc một tài liệu về toán học nào đó có giải thích về chúng mà là do đọc một … khổ thơ trong Truyện Kiều:
Một tay gây dựng cơ đồ
Bấy lâu bể Sở sông Ngô tung hoành
Bó thân về với triều đình
Hàng thần lơ láo phận mình ra đâu
Áo xiêm ràng buộc lấy nhau
Vào luồng ra cúi công hầu mà chi
Sao bằng riêng một biên thùy
Sức này đã dễ làm gì được nhau
Chọc trời khuấy nước mặc dầu
Dọc ngang nào biết trên đầu có ai …1
Khi đọc câu “Bấy lâu bể Sở sông Ngô tung hoành” mình thắc mắc “bể Sở sông Ngô” là gì và khi google thì có một kết quả tìm kiếm cho ra nghĩa của từ “tung hoành”: “Nói hành động dọc ngang, không chịu khuất phục”,2 lúc này mình vỡ lẽ, hóa ra “tung hoành” là “dọc ngang”. Té ra câu giang hồ hay nói “một thời tung hoành ngang dọc” là sai, mà đúng ra phải là “một thời tung hoành dọc ngang” :))
Thế đấy, thêm một ví dụ nữa cho thấy mình cần phải tự trau dồi vốn từ nói và văn học hơn nữa để hiểu toán học hơn 🙂 và sẽ không bao giờ quên “Tung là dọc, hoành là ngang”!
2. Trục dọc hay trục đứng?3
Khi định nghĩa về hệ trục tọa độ Oxy, một số tài liệu viết “Trục đứng được gọi là trục tung”, mình nghĩ dùng từ “trục đứng” không được hợp lý và tổng quát.
Không hợp lý là vì từ “đứng” thể hiện thuộc tính “độ cao” của đối tượng, trong khi nói hệ tọa độ Oxy thì hiển nhiên ta đang nói trên mặt phẳng, mà trên mặt phẳng thì chỉ có 2 chiều là chiều dài và chiều rộng hay chiều dọc và chiều ngang chứ không có chiều đứng/cao.
Không tổng quát là vì, nếu dùng từ “trục đứng” để nói về một trục trong hệ tọa độ Oxyz thì theo bạn trục nào trong hình vẽ dưới đây là trục đứng Oy và trục nào là trục cao Oz?
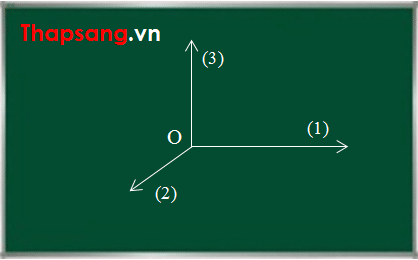
Trục nào là trục đứng Oy, trục nào là trục cao Oz?
Trong khi, nếu dùng các từ “trục ngang, trục dọc và trục cao” thì rõ ràng ta sẽ nói ngay trục (3) là trục cao Oz, trục (1) là trục ngang và trục (2) là trục dọc. Vì ngang là “ngang đường, ngang mắt”, dọc là “dọc đường, dọc theo mắt” và cao là “ngước cao”. 🙂
- Trích đoạn Kiều tự vẫn khi Từ Hải bị Hồ Tôn Hiến bao vây. Nguồn: Wikipedia [↩]
- Từ điển trực tuyến: vietdicts.com [↩]
- Mục này được bổ sung vào lúc 22h45′ ngày 25/06/2014 [↩]