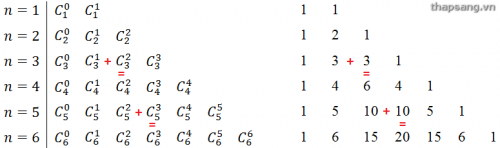Home » Dạy và học toán » Số tổ hợp và tính chất

Số tổ hợp và tính chất

Vận dụng thành thạo và linh hoạt các công thức về số tổ hợp là một kĩ năng cơ bản. Bài viết này mình chia sẻ với các bạn kinh nghiệm dạy và học về Số tổ hợp, và cách vận dụng linh hoạt các công thức Số tổ hợp thông qua một bài toán đơn giản.

Mặc dù có rất ít công thức về Số tổ hợp, nhưng các công thức của nó lại không dễ nhớ với học sinh và hay nhầm lẫn. Học sinh khó nhớ và hay nhầm lẫn ở 3 chỗ: Một là khó nhớ công thức, vì các công thức của số tổ hợp, cũng như chỉnh hợp được thường được giới thiệu trong sách giáo khoa ở dạng biểu diễn theo giai thừa với biểu thức “cồng kềnh”. Hai là, hay nhầm lẫn giữa công thức của số chỉnh hợp và tổ hợp. Ba là, hay quên điều kiện có nghĩa của các công thức.

  1. Ghi nhớ công thức
  2. Vận dụng công thức
  3. Toán học và tư duy

1. Ghi nhớ công thức số tổ hợp

Để giúp cho học sinh dễ nhớ các công thức, cách mình thường làm là yêu cầu học sinh phát biểu công thức dưới dạng lời (ý nghĩa). Ví dụ, với 2 công thức

C^k_n = C^{n-k}_n

C^k_n + C^{k+1}_n = C^{k+1}_{n+1}

Mình khai thác tối đa tính trực quan của Tam giác Pascal

Tam giác Pascal: Tổng hai số tổ hợp liên tiếp cùng hàng bằng số tổ hợp hàng dưới cùng cột

Tam giác Pascal: Tổng hai số tổ hợp liên tiếp cùng hàng bằng số tổ hợp hàng dưới cùng cột

Từ tam giác giác Pascal hướng dẫn học sinh phát biểu 2 công thức trên bằng lời:

  • C^k_n = C^{n-k}_n – Hai số tổ hợp cách đều hai đầu thì bằng nhau, rồi nói “gọn” lại là: Tính chất cách đều
  • C^k_n + C^{k+1}_n = C^{k+1}_{n+1} – Tổng hai số tổ hợp liên tiếp cùng hàng bằng số tổ hợp hàng dưới cùng cột.

Sau đó, cho học sinh áp dụng và ghi các công thức với một số trường hợp thường gặp. Ví dụ:

C^0_n=C^n_n = 1

C^1_n = C^{n-1}_n = n

C^2_n = C^{n-2}_n = \frac{n(n-1)}{2}

C^{n-k}_n=C^k_n

C^{k+1}_{n+1}=C^k_n + C^{k+1}_n

2. Vận dụng công thức

Ví dụ sau đây minh họa cách vận dụng 2 công thức trên vào một bài toán trong đề thi thử Đại học năm 2013 của trường THPT Chuyên Lý Tự trọng – Cần Thơ. Đề bài như sau:

Câu VII.a (1,0 điểm). Cho số tự nhiên n thỏa mãn C^{n-1}_n + C^{n-2}_n = 36 (C^k_n là số tổ hợp chập k của n). Tìm hệ số của x^8 trong khai triển thành đa thức của biểu thức f(x)=(1+2x^2-x^3)^n.

Để giải được bài toán trên, học sinh cần giải phương trình sau để tìm n:

C^{n-1}_n + C^{n-2}_n = 36

Lúc này, sẽ có nhiều lời giải khác nhau cho phương trình trên bởi các học sinh khác nhau. Sự khác nhau là do kiến thức và kĩ năng vận dụng. Chẳng hạn, với những học sinh nhớ được và biết vận dụng công thức số tổ hợp dưới dạng giai thừa thì sẽ trình bày lời giải như đáp án:

Giải:

* Xét phương trình C^{n-1}_n + C^{n-2}_n = 36\ (1). Điều kiện: 2\le n \in \mathbb{N}

* Khi đó

(1) \Leftrightarrow C^{n-1}_{n+1} = 36 \Leftrightarrow \frac{(n+1)!}{2(n-1)!}=36

\Leftrightarrow \frac{(n+1).n}{2} = 36 \Leftrightarrow n^2+n-72=0

\Leftrightarrow n = 8\ (tm) \vee n = -9\ (ktm)

Nhưng với học sinh khác thì có thể trình bày như sau:

Giải

* Xét phương trình C^{n-1}_n + C^{n-2}_n = 36\ (1). Điều kiện: 2\le n \in \mathbb{N}

* Khi đó

(1) \Leftrightarrow C^{n-1}_{n+1} = 36 \Leftrightarrow C^2_{n+1} = 36

\Leftrightarrow \frac{(n+1).n}{2} = 36 \Leftrightarrow n^2+n-72 = 0

\Leftrightarrow n = 8\ (tm) \vee n = -9\ (ktm)

Có gì khác nhau giữa hai lời giải

Bạn có thể nhận thấy ngay, sự khác nhau giữa hai lời giải là ở cách tính số C^{n-1}_{n+1}. Ở lời giải thứ nhất, học sinh đã áp dụng công thức tính số tổ hợp theo giai thừa:

C^k_n = \frac{n!}{k!(n-k)!}

cho số C^{n-1}_{n+1}, rồi áp dụng các tính chất của giai thừa để rút gọn. Còn ở lời giải thứ hai, học sinh đã quy C^{n-1}_{n+1} về số tổ hợp có chập bé hơn, nhờ công thức (Tính chất cách đều):

C^{n-k}_n=C^k_n

sau đó, vì chỉ số trên (chập) bằng 2 nên có thể áp dụng công thức (Tích hai số liên tiếp chia hai):

C^2_n = \frac{n(n-1)}{2}

3. Toán học và tư duy

Nếu bạn là học sinh thì có thể bạn sẽ cho rằng, giải thế nào trả được, miễn là ra đáp số và hơn nữa hai lời giải trên cũng không khác biệt mấy. Không có lời giải nào vượt trội hơn lời giải kia. Nhưng nếu bạn là giáo viên và có ý thức rèn tư duy cho học sinh thì bạn sẽ thấy rằng, cần tận dụng cơ hội này để hướng học sinh của mình giải theo cách thứ hai. Tại sao? Vì việc vận dụng công thức

C^{n-k}_n=C^k_n

không chỉ đơn thuần là để giải bài toán mà nó còn chứa đựng một lối suy nghĩ: “quy vấn đề phức tạp về vấn đề đơn giản hơn“.

Trong thực tế cũng như khoa học, thói quen suy nghĩ “quy vấn đề phức tạp về vấn đề đơn giản hơn” để giải quyết là rất cần thiết và quan trọng. Thói quen suy nghĩ đó không chỉ giúp tiết kiệm “sức lực, tài lực, thời gian” trong công việc mà còn là “định hướng” cho việc tìm kiếm giải pháp cho vấn đề. Thói quen đó sẽ trở nên sắc bén nếu được rèn luyện thường xuyên với sự hướng dẫn có chủ ý của giáo viên.



Thapsang.vn
Bài hay?Viết bình luận

Share
Xem tiếp bài có từ khóa

Mời bạn đón đọc các bài viết tiếp theo bằng cách đăng kí nhận bài viết mới qua email hoặc like fanpage Thapsang.vn để nhận được thông báo khi có cập nhật mới.

Có thể bạn muốn xem

Bài tập hàm số lớp 10

Số quy tròn và các hóa đơn

Quy tắc xét dấu logarit và ứng dụng

Tại sao lũy thừa với số mũ 0 lại bằng 1?

Phương trình lượng giác khácCâu 2 - giải phương trình lượng giác, năm nay dễ hơn năm ngoái
Comments: 6
  1. 11 years ago

    tam giác Pascal dựng theo hình như vậy rất khó nhìn, tại sao ko dựng theo hình tam giác đều đối xứng, ko chỉ có phép cộng ở dòng giữa như ở trên mà tổng của 2 hệ số liên tiếp bất kỳ ở dòng trên sẽ được 1 hệ số ở dòng dưới giữa 2 hệ số dòng trên ( trừ hệ số đầu và cuối là số 1 )

    ReplyCancel
  2. 11 years ago

    Chào bạn,

    Cảm ơn phản hồi của bạn. Mình biết, có thể vẽ tam giác Pascal theo dạng tam giác cân như bạn nói và có thể nó dễ nhìn hơn dạng tam giác vuông như mình vẽ trên. Tuy nhiên, mình chọn cách vẽ dạng tam giác vuông vì một số lí do sau:

    1) Dạng này cho phép biểu diễn các số tổ hợp có cùng số chập thành một cột thẳng đứng.

    2) Nhờ các số tổ hợp có cùng chập được xếp thành 1 cột nên dạng tam giác vuông thể hiện rõ "ý nghĩa" của công thức $$C^{k-1}_n + C^k_n = C^k_{n+1}$$ hơn. Cụ thể là, "Tổng hai số tổ hợp liên tiếp cùng hàng bằng số tổ hợp hàng dưới cùng cột", như được minh họa trong hình vẽ. Dạng tam giác cân không thể hiện được điều này, vì các số tổ hợp có cùng chập không được xếp thành 1 cột.

    Thực tế, học sinh rất khó nhớ và hay quên công thức tổng hai số tổ hợp, nên nếu vẽ dạng tam giác vuông và phát biểu công thức dưới dạng lời văn như trên thì sẽ giúp học sinh dễ nhớ khi vận dụng.

    3) Khi vẽ tam giác Pascal gồm các điểm ứng với các số tổ hợp thì dạng tam giác vuông sẽ dễ vẽ hơn dạng tam giác cân. Vì dạng tam giác vuông được căn trái, nên cứ viết lần lượt từ trái qua phải và thẳng cột là xong, còn dạng tam giác cân thì phải căn giữa nên khi vẽ phải ước lượng vị trí của số đầu tiên trên một hàng để đảm bảo tính cân xứng của tam giác.

    Trân trọng,

    ReplyCancel
  3. 11 years ago

    Tổng quát, ta có thể phát biểu công thức

    $$C^k_n = \frac{A^k_n}{k!}=\frac{n(n-1)…(n-k+1)}{k.(k-1)…2.1}$$

    Nhận xét:

    * Chập của hệ số tổ hợp là $$k$$ thì cả tử và mẫu đều là tích của $$k$$ thừa số liên tiếp

    * Tử là tích của k thừa số liên tiếp giảm từ n còn mẫu là tích của k số liên tiếp giảm từ k

    Như vậy:

    * Chập bao nhiêu tích bấy nhiêu?

    * Có thể phát biểu bằng lời cho dễ nhớ và dễ tính số $$C^k_n$$ là “Tích $$k$$ số liên tiếp giảm từ $$n$$ chia cho tích $$k$$ số liên tiếp giảm từ $$k$$” Ổn không nhỉ?

    Chi tiết xem thêm bài viết: Cách tính nhẩm số tổ hợp

    ReplyCancel
  4. dạt phạm
    10 years ago

    cho em hỏi tại sao trong công thức tính tổ hợp chập k của n phần tử \[C^k_n = \frac{A^k_n}{k!}=\frac{n(n-1)…(n-k+1)}{k.(k-1)…2.1}\] luôn là số nguyên?

    ReplyCancel
    • 10 years ago

      Tôi nghĩ câu hỏi của em có lẽ phải là:

      “Tại sao tỉ số $$\frac{A^k_n}{k!}$$ luôn là số nguyên?”

      Câu trả lời ngắn gọn:

      1) Theo định nghĩa, $$C^k_n$$ là “số tổ hợp chập $$k$$ của $$n$$” nên $$C^k_n$$ là số nguyên.

      2) Mặt khác, chứng minh được $$C^k_n=\frac{A^k_n}{k!}$$

      Từ (1)(2) suy ra tỉ số $$\frac{A^k_n}{k!}$$ là số nguyên.

      Cũng có thể chứng minh trực tiếp tỉ số

      \[\frac{n(n-1)…(n-k+1)}{k.(k-1)…2.1}\]

      là số nguyên mà không cần khai thác định nghĩa về số $$C^k_n$$. Em thử xem.

      ReplyCancel
  5. yến ciu
    9 years ago

    Thầy cô cm cho e công thức PA-XCAN với ạ…e cảm ơn thầy cô nhiu

    ReplyCancel

Để lại một bình luận

Thapsang.vn

Chào bạn, Thapsang.vn – nơi chia sẻ các thông tin, kiến thức bổ ích về giáo dục và công nghệ, hoạt động từ 10/2012 đến nay. Hi vọng bài viết này có ích cho bạn và mong nhận được nhiều phản hồi của bạn. Cảm ơn bạn đã đọc bài viết!

12 years ago 6 Comments Dạy và học toán, , 16,849