Giới hạn – cái biến điều không thể thành có thể

Giới hạn – một chủ đề rất quan trọng trong nội dung môn toán THPT, phần lớn được trình bày trong sách Đại số và Giải tích lớp 11. Khi dạy, bạn đã dẫn nhập vào chương này1 như thế nào? Còn sau đây là cách mình hay làm.

1. 1. Dẫn nhập
2. 2. Kích thích thêm
3. 3. Cách dẫn nhập của bạn?

1. Dẫn nhập

Chúng ta dễ dàng tính ngay được tổng sau

thế còn tổng này thì sao?

Sự khác biệt giữa 2 tổng và là gì? Có tính được tổng không?

Quá đơn giản, là một tổng hữu hạn còn là một TỔNG VÔ HẠN. Tính một tổng vô hạn ư? Thật không tưởng! Đúng vậy, đó là một điều không thể với những ai chưa học chương này. Giới hạn – cái biến điều không thể thành có thể. Trước tiên, chúng ta cùng tìm hiểu “Giới hạn của dãy số” là gì? – Bài 1. Giới hạn dãy số.

2. Kích thích thêm

Để vấn đề trở nên hấp dẫn hơn và kích thích hơn sự tò mò của học sinh, mình minh họa một cách trực quan cho học sinh thấy ngay rằng tổng có thể tính được, chính xác là bằng 1 và đặt vấn đề tính tổng này một cách chặt chẽ bằng toán học.

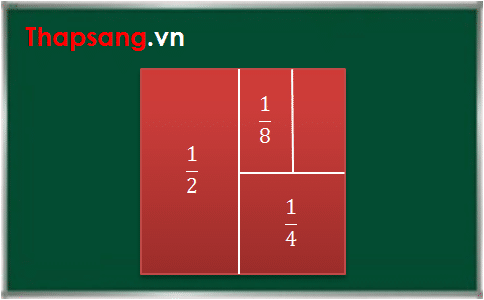
Mô tả trực quan: Xét một hình vuông có cạnh bằng 1. Chia đôi hình vuông này thành 2 phần bằng nhau, ta được mỗi phần có diện tích bằng 1/2. Tiếp tục chia đôi 1 phần thu được, ta được 2 phần mới, mỗi phần có diện tích là 1/4. Cứ tiếp tục chia mãi, chia mãi như thế, ta thu được vô số các hình chữ nhật mà tổng diện tích của các hình chữ nhật đó lại bằng 1 – diện tích hình vuông ban đầu.2

Đặt vấn đề: Đó là cách tính tổng bằng mô tả trực quan, còn làm thế nào để tính tổng đó một cách chặt chẽ bằng toán học?

3. Cách dẫn nhập của bạn?

Bạn đã dẫn nhập chủ đề này như thế nào? Hãy chia sẻ nó vào hộp bình luận phía dưới nhé!

Mời bạn đón đọc các bài viết tiếp theo bằng cách đăng kí nhận bài viết mới qua email hoặc like fanpage Thapsang.vn để nhận được thông báo khi có cập nhật mới.

1. Lý luận phương pháp dạy học gọi là gợi động cơ học tập [↩]
2. Ví dụ này được giới thiệu trong phần đọc thêm của chương, trong SGK đã nói trên [↩]