Qua hai bài viết trước, bạn đã biết: “Câu 2 của năm nay dễ hơn” và “Câu 4 của năm ngoái khó hơn“. Bài viết này, tôi và bạn cùng phân tích xem “Câu 5 của năm nay dễ hơn hay khó hơn so với năm ngoái”?
Lời nhắn: Bài viết khá dài và nội dung khá sâu, đòi hỏi bạn phải có một số kiến thức và trình độ nhất định về Hình học không gian, vì có những ý tôi không thể viết chi tiết hơn, viết chi tiết hơn thì bài viết sẽ quá dài và bị loãng. Bạn cũng cần một khoảng thời gian đủ lâu để đọc và suy luận, do đó nếu bạn thật sự muốn biết vì sao kết luận của bài viết lại là xyz 😀 thì mới đọc, còn không thì lời khuyên cho bạn là “Hãy kéo thanh cuộn dọc xuống cuối bài viết và đọc luôn kết luận”, đỡ mất thời gian và “nặng đầu”. 😀
Câu 5, một câu về Hình học không gian. Đề bài của năm ngoái và năm nay như sau:
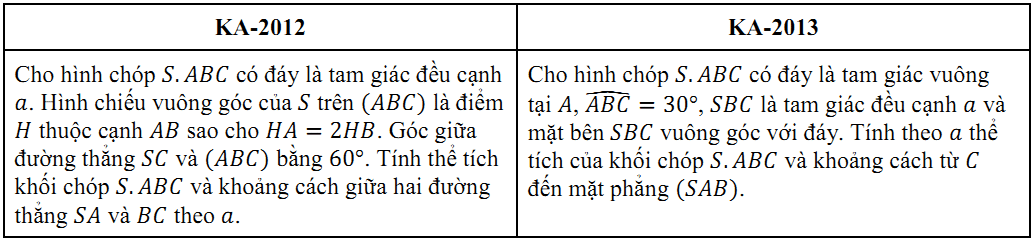
Điều thú vị là giả thiết của cả hai câu đều cho một hình chóp tam giác và kết luận cũng gồm 2 ý “giông giống” nhau, ý thứ nhất cùng là tính thể tích của khối chóp có “tên” 
và ý thứ hai là tính khoảng cách. Do đó, tôi sẽ so sánh từng ý với nhau. Đầu tiên, tính thể tích.
Tính thể tích khối chóp
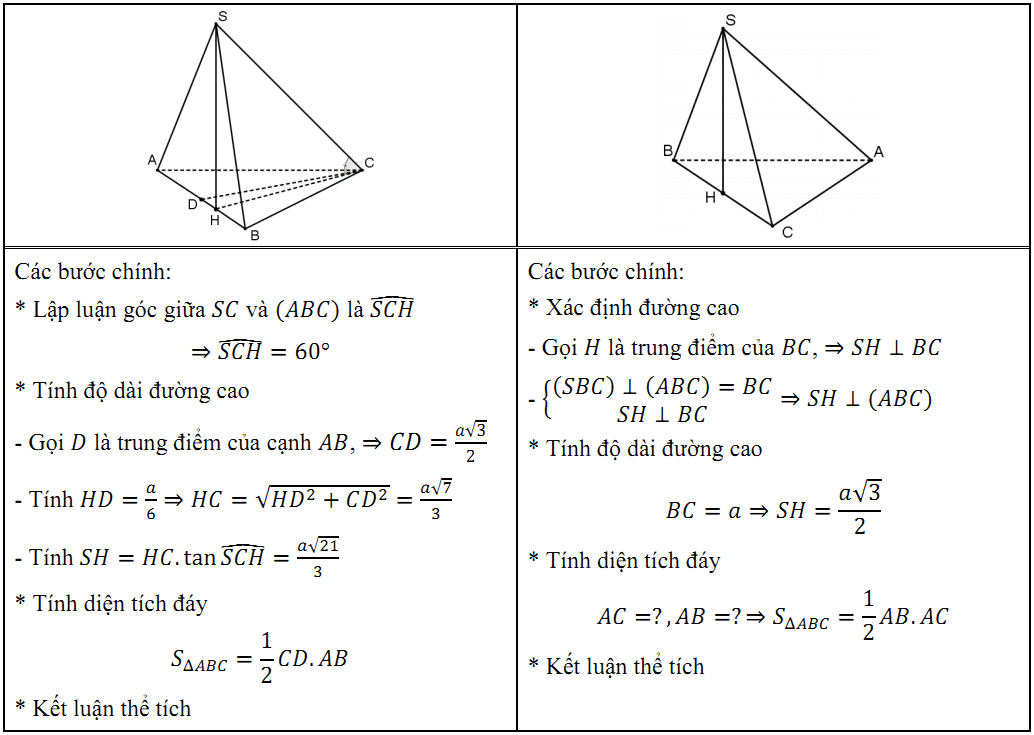
Phân tích:
– Về độ khó của bước đầu tiên: xác định đường cao của đề thi năm nay so với xác định góc của đề thi năm ngoái là ngang nhau. Vì dạng hình chóp có 1 mặt bên vuông góc với đáy, hơn nữa mặt bên đó lại là 1 tam giác đều, là khá quen thuộc với học sinh lớp 12 khi ôn tập thi tốt nghiệp và tuyển sinh đại học – cao đẳng.
– Sự chênh lệch bắt đầu ở bước tính đường cao của hình chóp. Như bạn thấy trong bảng trên, việc tính độ dài đường cao của đề năm ngoái đòi hỏi thí sinh phải phát hiện, suy luận và thực hiện các bước tính toán nhiều hơn so với việc “gần như là có sẵn” của đề năm nay.
– Bước tính diện tích đáy: Tự bạn đánh giá nhé! 🙂
Kết luận: Ý này của đề năm ngoái đòi hỏi thí sinh có trình độ suy luận cao hơn.
Chúng ta sang ý thứ hai. Ở ý thứ hai thì câu hỏi của năm ngoái và năm nay có sự khác biệt một chút, một đằng yêu cầu tính khoảng cách giữa hai đường thẳng chéo nhau, còn một đằng yêu cầu tính khoảng cách từ một điểm đến một mặt phẳng.
Tính khoảng cách
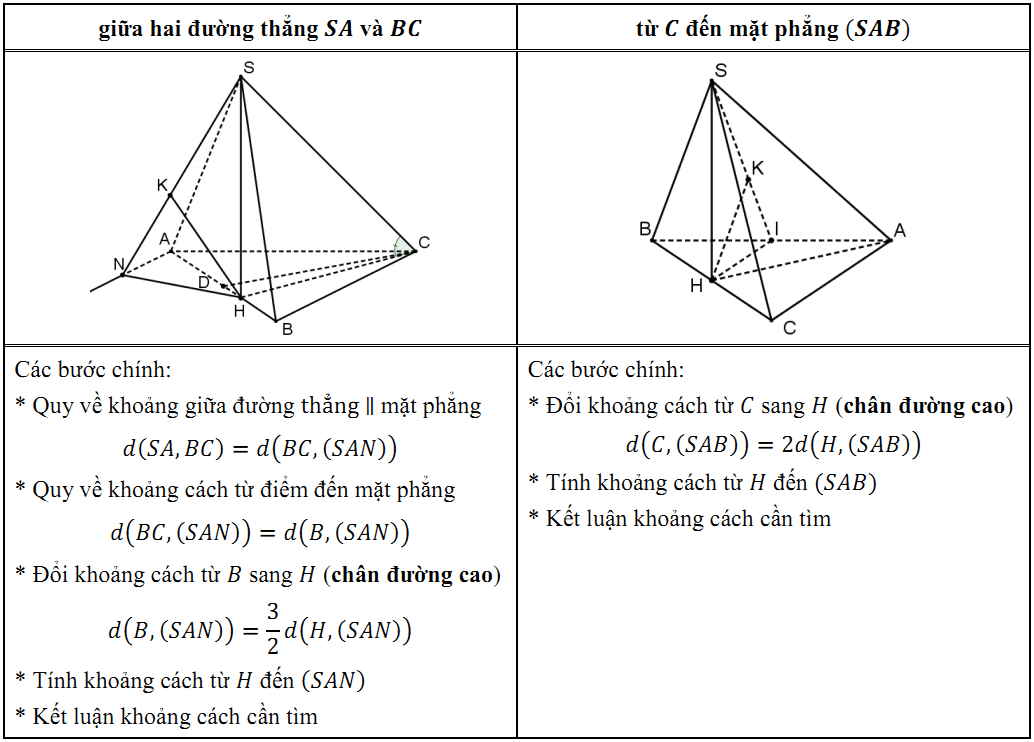
“Chỉ một chút thôi, nhưng đã khác biệt rồi” :D, nên chúng ta sẽ cần phân tích chi tiết hơn cho từng năm.
Các cách giải chính ở đề năm nay
– Ở đề thi năm nay, để tính khoảng cách từ điểm 
đến mặt phẳng 
có hai cách giải chính. Cách thứ nhất là “Ứng dụng thể tích để tính khoảng cách” và cách thứ hai là “Tính trực tiếp hoặc đổi khoảng cách”.
– Theo cách thứ nhất, bạn “coi” khoảng cách cần tính từ đến 
là chiều cao từ đỉnh của hình chóp 
tới mặt đáy . Bạn có 
, mà thể tích của khối chóp đã xác định nên bạn chỉ cần tìm diện tích của tam giác 
. Đây là cách được giới thiệu trong đáp án của Bộ Giáo dục và đào tạo, nếu bạn quên thì có thể xem lại trên Thư viện Đề thi – VLOS: Toán ĐH-KA – 2013
– Theo cách thứ hai, hướng mà đa số thí sinh sẽ dùng là “Đổi khoảng cách từ sang 
”. Đây là một kỹ thuật tính khoảng cách khá cơ bản. Thí sinh chỉ cần lập luận do là trung điểm của 
nên có 
. Các bước chính của cách này được minh họa trong bảng trên và được cụ thể hóa trong bảng dưới đây.
– Thực hiện theo cách nào là tùy thuộc vào trình độ và thói quen tư duy của thí sinh:
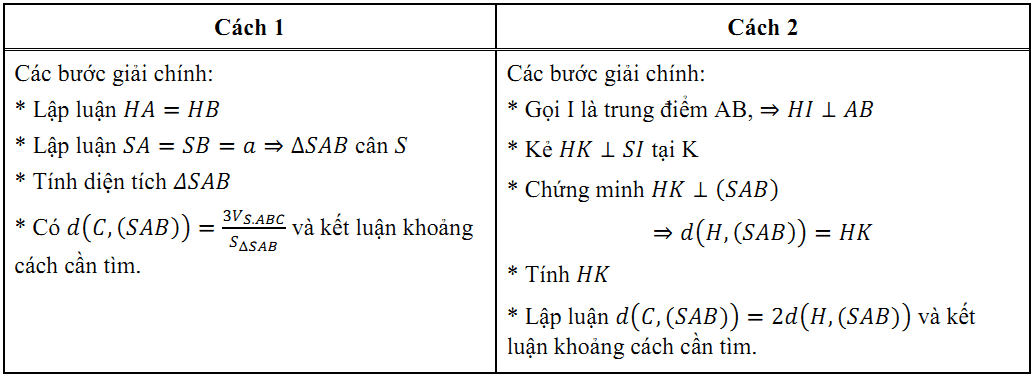
Nếu thí sinh phát hiện và giải bài toán theo cách thứ nhất thì sẽ nhanh chóng ra kết quả hơn so với cách thứ hai. Nếu thực hiện lời giải theo cách thứ 2 thì sẽ dài hơn, đòi hỏi phải tiến hành nhiều thao tác nhỏ hơn, mặc dù khối lượng tính toán có phần nhẹ hơn do 
là trung điểm 
. Tuy nhiên, dù thực hiện theo cách nào thì việc suy luận và tính toán với “Bài toán 3: Tính khoảng cách từ một điểm đến một mặt phẳng” ở đề năm nay vẫn là đơn giản hơn nhiều so với “Bài toán 1: Tính khoảng cách giữa hai đường thẳng chéo nhau” ở đề năm ngoái.
Cách giải chính ở đề năm ngoái
– Để giải “Bài toán 1: Tính khoảng cách giữa hai đường thẳng chéo nhau” thì cách hay được dùng là quy về “Bài toán 2: Tính khoảng cách giữa một đường thẳng song song với một mặt phẳng”, sau đó tiếp tục quy về “Bài toán 3: Tính khoảng cách từ một điểm đến một mặt phẳng”. Như vậy, nếu giải đề năm nay thí sinh chỉ cần thực hiện Bài toán 3 thì ở đề năm ngoái thí sinh phải giải quyết “Bài toán 1” – bài toán rộng hơn, lớn hơn.
– Vốn dĩ Bài toán 1 đã khó hơn, vậy mà ở đề năm ngoái, để đưa được về Bài toán 2, thí sinh phải có một trình độ “kha khá” thì mới có thể nhìn ra rồi dựng đường thẳng qua 
và song song với (Chứ không dựng đường thẳng qua 
hay và song song với 
. Tại sao à? Bạn thử làm xem!), từ đó tạo ra mặt phẳng 
song song với .
– Đến lúc đưa được Bài toán 2 về Bài toán 3 và quy về bài toán khoảng cách cơ bản (Tính khoảng cách từ chân đường cao đến mặt bên) thì ngay cả ở bước tính toán, đề thi năm ngoái cũng khó khăn hơn, do điểm 
không là điểm đặc biệt như trung điểm của đề năm nay.
Tóm lại, ở cả hai ý của câu 5 của đề năm ngoái không những đòi hỏi thí sinh phải có một khả năng quan sát tốt, một trình độ tư duy sắc bén mà còn đòi hỏi cả kĩ năng tính toán cao hơn nhiều so với đề năm nay.
Ps: Bạn thật là may nếu bạn thi năm nay! 🙂
Để lại một bình luận