Mình mới đọc một bài toán về cấp số cộng và cấp số nhân và giải nó thì thấy hay hay, nên ghi lại để các bạn cùng SOI và MỔ (Mà MỔ rồi mới SOI cũng được, đừng liên tưởng tới ngành y nhé)
Nội dung nổi bật: Khai thác tính chất 3 số hạng liên tiếp của cấp số cộng và cấp số nhân để giải toán. Bài viết phù hợp với các bạn học sinh lớp 11 trở lên. Nếu bạn chưa biết cấp số cộng, cấp số nhân là gì thì nên … Google rồi mới đọc tiếp 🙂

Tính chất của 3 số hạng liên tiếp trong một cấp số
Bài toán của chúng ta như sau:
1. Bài toán
Cho 4 số nguyên dương, trong đó 3 số đầu theo thứ tự lập thành một cấp số cộng, 3 số sau lập thành một cấp số nhân. Biết tổng số hạng đầu và cuối là 37, tổng 2 số hạng giữa là 36. Tìm 4 số đó?
2. Phân tích
* Chúng ta cần tìm 4 số, một cách tự nhiên, cần tìm gì thì gọi đấy (một bài học mà các “sư phụ” vẫn dạy chúng ta khi còn ở … “Võ đường THCS”) 😀 . Giả sử ![]() theo thứ tự là 4 số cần tìm. Giờ từ giả thiết, chúng ta cần thiết lập các phương trình quan hệ giữa chúng.
theo thứ tự là 4 số cần tìm. Giờ từ giả thiết, chúng ta cần thiết lập các phương trình quan hệ giữa chúng.
* Theo giả thiết
– vì 3 số hạng đầu là một cấp số cộng nên ![]() 1
1
– vì 3 số hạng sau là một cấp số nhân nên ![]() 2
2
– vì tổng số hạng đầu và cuối là 37 nên ![]()
– vì tổng 2 số hạng giữa là 36 nên ![]()
* Từ đó ta có hệ 4 phương trình, 4 ẩn:
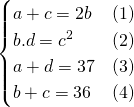
* Làm thế nào để giải hệ này? Thoạt nhìn, trông cũng hơi “lằng nhằng”. Hãy bình tĩnh 🙂 , bình tĩnh thì mới nhớ được nguyên tắc chung để giải hệ phương trình nhiều ẩn là phải tìm từng ẩn một. Muốn thế, phải chọn một ẩn và biểu diễn các ẩn còn lại về ẩn đã chọn. Vậy, chúng ta chọn ẩn nào? Ẩn ![]() hay
hay ![]() hay
hay ![]() hay
hay ![]() ?
?
* Chọn ẩn nào thì cũng đều ra kết quả cả, tuy nhiên sự khác biệt là ở độ phức tạp và khối lượng tính toán. (“Mọi con đường đều dẫn đến thành Rome”, tuy nhiên có những con đường thẳng và cũng có những con đường … cong. Nhưng chắc chắn sẽ không có con đường … “cong Trường Chinh”) 😀 .
– Nếu bạn chọn ẩn ![]() hay
hay ![]() thì phải sẽ phải rút
thì phải sẽ phải rút ![]() theo chúng và khi thay vào phương trình (2) bạn sẽ phải thực hiện phép nhân ở vế trái và cả phép bình phương ở phải.
theo chúng và khi thay vào phương trình (2) bạn sẽ phải thực hiện phép nhân ở vế trái và cả phép bình phương ở phải.
– Nhưng, nếu bạn chọn ![]() và rút ba ẩn còn lại theo
và rút ba ẩn còn lại theo ![]() thì khi thay vào phương trình (2), bạn chỉ cần thực hiện phép nhân ở vế trái mà thôi!! (giảm khối lượng công việc phải làm, tiết kiệm được không nhỏ: thời gian + sức lực + giấy + mực, thông minh nhờ) 😀
thì khi thay vào phương trình (2), bạn chỉ cần thực hiện phép nhân ở vế trái mà thôi!! (giảm khối lượng công việc phải làm, tiết kiệm được không nhỏ: thời gian + sức lực + giấy + mực, thông minh nhờ) 😀
* Từ (4) suy ra ![]() , thay vào (1) có
, thay vào (1) có ![]() , thay tiếp vào (3) có
, thay tiếp vào (3) có ![]()
* Thay ![]() vào (2) ta được
vào (2) ta được
![]()
* Từ đó tìm được ![]() và
và ![]()
* Kết luận: 4 số cần tìm là ![]() hoặc
hoặc ![]()
3. Lời giải
* Giả sử ![]() theo thứ tự là 4 số cần tìm
theo thứ tự là 4 số cần tìm
* Theo giả thiết ta có
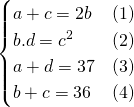
* Từ (4) suy ra ![]() , thay vào (1) có
, thay vào (1) có ![]() , thay tiếp vào (3) có
, thay tiếp vào (3) có ![]()
* Thay ![]() vào (2) ta được
vào (2) ta được
![]()
* Với ![]()
* Với ![]()
* Vậy, 4 số cần tìm là: ![]() hoặc
hoặc ![]()
4. Đào sâu, nghĩ lâu 😀
* Vì 3 số hạng liên tiếp của một cấp số luôn được biểu diễn theo một phương trình, nên nếu biết 2 trong ba số thì sẽ xác định được số còn lại. Chẳng hạn
– nếu ![]() và
và ![]() là số thứ nhất và số thứ hai của một cấp số cộng thì số thứ ba là
là số thứ nhất và số thứ hai của một cấp số cộng thì số thứ ba là ![]()
– nếu ![]() và
và ![]() là số thứ nhất và số thứ hai của một cấp số nhân thì số thứ ba là
là số thứ nhất và số thứ hai của một cấp số nhân thì số thứ ba là ![]()
* Như vậy, với một cấp số có 3 số hạng thì “chỉ cần biết 2 số hạng là đủ” (Chỉ 2 là đủ – câu này quen quen … “Dù gái hai trai, chỉ 2 là đủ” 😀 ). Do đó, ta có thể trình bày cách giải bài toán trên theo một cách khác.
5. Cách khác
Thay vì gọi 4 ẩn cho 4 số cần tìm, ta chỉ cần gọi 2 ẩn cho 2 số hạng của cấp số cộng hoặc cấp số nhân thì 2 số hạng còn lại sẽ được biểu diễn theo chúng. Cụ thể
* Giả sử ![]() và
và ![]() là số hạng thứ nhất và thứ hai cần tìm.3
là số hạng thứ nhất và thứ hai cần tìm.3
* Do 3 số hạng đầu là cấp số cộng nên số hạng thứ ba là: ![]()
* Mà 3 số hạng cuối là một cấp số nhân nên số hạng thứ tư là: ![]() (Chú ý:
(Chú ý: ![]() vì nếu
vì nếu ![]() thì 3 số hạng của cấp nhân phải là
thì 3 số hạng của cấp nhân phải là ![]() . Vô lí, vì tổng hai số hạng giữa phải bằng 36)
. Vô lí, vì tổng hai số hạng giữa phải bằng 36)
* Vậy 4 số cần tìm có dạng: ![]()
* Theo giả thiết ta có
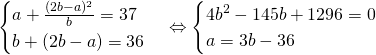
* Từ hệ này tìm được ![]() và 2 số hạng còn lại!
và 2 số hạng còn lại!
Bình luận: Cách này “gọn gàng” đấy chứ, bạn có nghĩ như vậy không?
Nếu bạn có một cách giải khác nữa thì chia sẻ với minh nhé, hãy gõ nó vào hộp bình luận dưới đây. Cảm ơn bạn!
- Tính chất đặc trưng của 3 số hạng liên tiếp trong một cấp số cộng: Số hạng đứng giữa bằng trung bình cộng của số đứng trước và số đứng sau. [↩]
- Tính chất đặc trưng của 3 số hạng liên tiếp trong một cấp số nhân: Giá trị tuyệt đối của số hạng đứng giữa bằng trung bình nhân của số đứng trước và đứng sau [↩]
- Phần này được cập nhật lại ngày 23/04/2014. Bản đầu tiên mình giả sử c và d là hai số hạng thứ ba và thứ tư dẫn đến lời giải hơi rắc rối 🙂 [↩]


