“Tại sao cơ số của lũy thừa với số mũ hữu tỉ phải dương?”, đó là câu hỏi mà một học sinh lớp 12 có thể đặt ra khi học về định nghĩa lũy thừa với số mũ hữu tỉ1:
[latexpage]
Cho $a$ là một số thực dương và $r$ là một số hữu tỉ. Giả sử $r=\frac{m}{n}$, trong đó $m$ là một số nguyên còn $n$ là một số nguyên dương. Khi đó, lũy thừa của $a$ với số mũ $r$ là số $a^r$ xác định bởi $a^r=a^{\frac{m}{n}}=\sqrt[n]{a^m}$
Một câu hỏi mà học sinh không dễ trả lời, sách giáo khoa lại không có dòng nào “gợi mở” về chi tiết này, các tài liệu tham khảo thì lại càng không2, còn ở trên lớp thì các thầy cô giáo lại không có đủ thời gian để hướng dẫn và không phải học sinh nào cũng có khả năng khám phá vấn đề. Đó là những lí do khiến bài viết này ra đời.

Nếu bạn vẫn còn đọc đến đây, chào mừng bạn, một người tò mò và ham khám phá, hy vọng bài viết thú vị với bạn. 🙂
Quay lại với câu hỏi, tại sao định nghĩa đó chỉ áp dụng với cơ số dương mà không áp dụng cho cơ số âm? Với cơ số âm thì có vấn đề gì chăng? Đúng vậy, với cơ số âm thì sẽ có không ít vấn đề. Cụ thể:
Nếu lũy thừa $a^r=a^{\frac{m}{n}}=\sqrt[n]{a^m}$ cũng được định nghĩa đối với cả $a<0$ và $a^r$ cũng có các tính chất như lũy thừa với số mũ nguyên thì định nghĩa sẽ tự mâu thuẫn hoặc mâu thuẫn với tính chất.
Thật vậy, chúng ta cùng xem.
1. Định nghĩa lũy thừa tự mâu thuẫn
Tình huống thứ nhất, định nghĩa tự mâu thuẫn. Cụ thể, khi áp dụng định nghĩa cho một lũy thừa mà số mũ được biểu diễn bởi hai phân số khác nhau thì lại thu được 2 kết quả khác nhau. Chẳng hạn, xét lũy thừa $(-1)^{\frac{1}{3}}$.
Một mặt, theo định nghĩa ta có $(-1)^{\frac{1}{3}}=\sqrt[3]{(-1)^1}=-1$
Mặt khác, do $\frac{1}{3}=\frac{2}{6}$ nên $(-1)^{\frac{1}{3}}=(-1)^{\frac{2}{6}}$. Áp dụng định nghĩa ta lại có $(-1)^{\frac{2}{6}}=\sqrt[6]{(-1)^2}=1$
Như vậy, từ định nghĩa ta chứng minh được $-1=1$ 😀
\[-1=\sqrt[3]{-1}=(-1)^{\frac{1}{3}}=(-1)^{\frac{2}{6}}=\sqrt[6]{(-1)^2}=1\]
Có thể nói, trong tình huống này định nghĩa với cơ số âm đã tự mâu thuẫn.
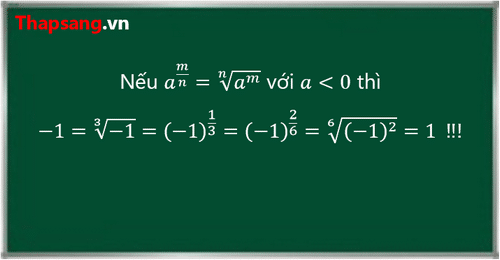
2. Định nghĩa mâu thuẫn với tính chất
Mặt khác, nếu vừa chấp nhận lũy thừa với số mũ hữu tỉ được định nghĩa cho cả cơ số âm và vừa muốn nó có tính chất như lũy thừa với số mũ nguyên thì sẽ có mâu thuẫn giữa định nghĩa với tính chất.
Ví dụ, cùng một bài toán tính lũy thừa, nhưng áp dụng định nghĩa thì cho một kết quả và áp dụng tính chất thì lại cho một kết quả khác. Chẳng hạn, tính lũy thừa sau $\left ( (-1)^{\frac{2}{3}} \right )^{\frac{3}{2}}$.
Theo định nghĩa ta có \[\left ( (-1)^{\frac{2}{3}} \right )^{\frac{3}{2}}=\left ( \sqrt[3]{(-1)^2} \right )^{\frac{3}{2}}=\sqrt{\left ( \sqrt[3]{(-1)^2} \right )^3}=\sqrt{(-1)^2}=1\]
Nhưng theo tính chất $(a^p)^q=a^{pq}$ thì ta lại có \[\left ( (-1)^{\frac{2}{3}} \right )^{\frac{3}{2}}=(-1)^{\frac{2}{3}\cdot \frac{3}{2}}=(-1)^1=-1\]
Như vậy, giống như tình huống trên, ta cũng chứng minh được $-1=1$ 😀
\[-1=(-1)^1=(-1)^{\frac{2}{3}\cdot \frac{3}{2}}=\left ( (-1)^{\frac{2}{3}} \right )^{\frac{3}{2}}\]
\[=\left ( \sqrt[3]{(-1)^2} \right )^{\frac{3}{2}}=\sqrt{\left ( \sqrt[3]{(-1)^2} \right )^3}=\sqrt{(-1)^2}=1\]
Chứng minh được $-1=1$ đã giỏi, lại còn bằng hai cách thì quả là giỏi quá xá, há há 😀
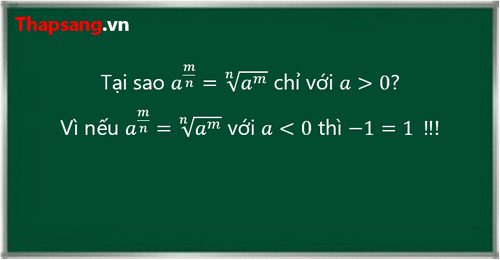
Tóm lại, để tránh những tình huống mâu thuẫn như trên và để lũy thừa với số mũ hữu tỉ có các tính chất như lũy thừa với mũ nguyên thì định nghĩa $a^r=a^{\frac{m}{n}}=\sqrt[n]{a^m}$ chỉ áp dụng cho $a>0$.
3. Bình luận
* “Tại sao cơ số của lũy thừa với số mũ hữu tỉ phải dương?” là một câu hỏi có tính lật ngược vấn đề, đặt được câu hỏi này cho thấy học sinh có tư duy độc lập và phản biện. Một phẩm chất tư duy đáng quý.
* Bài viết chỉ đề cập đến định nghĩa với cơ số âm mà không xét với cơ số bằng 0, bạn có biết tại sao không?
* Chú ý rằng, không chỉ với lũy thừa với số mũ hữu tỉ, tổng quát hơn ta biết rằng định nghĩa lũy thừa với số mũ không nguyên cũng chỉ áp dụng với cơ số dương. Bạn có thể tự giải thích được không?
* Ngoài những tình huống mâu thuẫn như trên, nếu bạn biết một tình huống mâu thuẫn khác, xin hãy chia sẻ nó vào hộp bình luận phía dưới nhé, cảm ơn bạn!

