Lâu rồi không đọc sách Hình học THCS, vừa đọc vừa làm ngẫu nhiên một vài bài thấy hay hay. Dưới đây là một bài toán có đề bài khá ngắn và cách mình phân tích, tìm tòi lời giải bài toán này.
Bài toán
Cho hình vuông ABCD. Gọi E, F lần lượt là trung điểm của BC và CD. Chứng minh rằng AE vuông góc với BF.
Phân tích
* Thông thường, muốn chứng minh hai đường thẳng vuông góc với nhau ta chứng minh góc tạo bởi chúng là vuông hoặc áp dụng các định lí quan hệ giữa song song và vuông góc. Do bài toán không chứa đựng yếu tố song song nên mình lựa chọn hướng thứ nhất.
* Nhưng, để chứng minh một góc bằng 
hay rộng hơn là để tính một góc thì ta cần xem xét nó là một góc của tam giác nào đó. Với đề bài trên, ta có 2 lựa chọn: Xét tam giác ABG chứa góc AGB hoặc tam giác BEG chứa góc BGE.
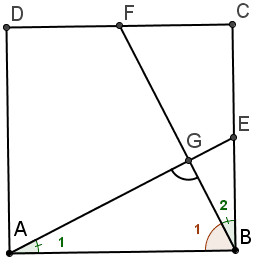
* Trong hai tam giác này, chọn tam giác nào? Mình chọn tam giác ABG vì tam giác này gần với giả thiết hơn tam giác kia. Why? Bạn thắc mắc à? Cứ suy nghĩ đi nhé, nếu cần thì cứ gõ ý kiến vào hộp bình luận ở phía dưới 😀
* Giờ tập trung vào việc chứng minh góc AGB bằng . Chúng ta có nhiều cách để chứng minh một góc nào đó là vuông, như dùng tỉ số lượng giác, định lý Pitago hoặc đi chứng minh tổng hai góc 
và 
là ,… Rõ ràng, lựa chọn thứ nhất và thứ hai là “khá u ám”, vì ta chưa nhìn thấy quan hệ giữa các cạnh AG và BG với các cạnh của hình vuông. Do đó, ta sẽ ưu tiên lựa chọn chứng minh 
trước.
* Do ABCD là hình vuông, nên 
, điều này gợi ý ta chứng minh 
là bài toán được giải quyết.
* Từ bài toán ban đầu giờ ta chỉ cần giải một bài toán khá quen thuộc “Chứng minh hai góc bằng nhau”. Thật quá dễ dàng, ai chả biết “Để chứng minh hai góc thậm chí hai đoạn nào đó bằng nhau thì phải nghĩ đến ngay việc chứng minh hai tam giác tương ứng chứa chúng là bằng nhau”.
* Quá rõ ràng, xét tam giác ABE và tam giác BCF có AB=BC, B=C, BE=CF. Vậy hai tam giác bằng nhau, suy ra hai góc .
Bài toán đã xong, giờ chỉ cần trình bày lại là có lời giải thôi. Bạn tự hoàn thiện nhé!
Cuối cùng, bạn có thể trình bày một cách giải khác với quá trình phân tích để tìm ra lời giải khác đó của bạn không?
Cảm ơn bạn.
Không có chi 🙂
Bài này nếu học xong lớp 10 có thể dụng vecto. Một cách cm 2 đường thẳng vuông góc vs nhau .
Bài toán này thường ẩn chứa trong các bài toán về Hình học không gian (câu 5 trong các đề thi TS ĐH-CĐ), khi đáy của một hình chóp hay lặng trụ là hình vuông. Vì vậy nên rèn cho học sinh thành thạo phương pháp chứng minh hình học Ơ-clit (như trên), nếu có điều kiện đào sâu thêm phương pháp vectơ hay tọa độ thì cũng tốt.
Anh dùng phương pháp toạ độ hoá cũng rất thú vị.