Một số sai lầm thường gặp khi giải toán và cách sửa (p5)

Bạn đang xem phần 5 / 5 của series Sai lầm thường gặp.

Hôm nay mình cho các cháu lớp 12 làm một bài “dễ như ăn kẹo” dưới đây, thế mà hầu hết “chúng nó” lại mắc sai lầm mới lạ chứ.

Đề bài
Lời giải của “bọn chúng”
Hồn nhiên
Sai ở đâu?
Tại sao mắc sai lầm?
Sửa như thế nào?
Bình luận

1. Đề bài

Cho hàm số $y=-x^3 + 3x^2 - 1$ có đồ thị $(C)$

a) Khảo sát sự biến thiên và vẽ đồ thị của hàm số

b) Tìm $m$ để phương trình $\frac{1}{3}x^3 - x^2 + m^2 = 0$ có ba nghiệm phân biệt

2. Lời giải của “bọn chúng”

“Chúng nó” làm câu a ngon lành và vẽ được cái đồ thị đẹp “gần được” như thế này: 😀

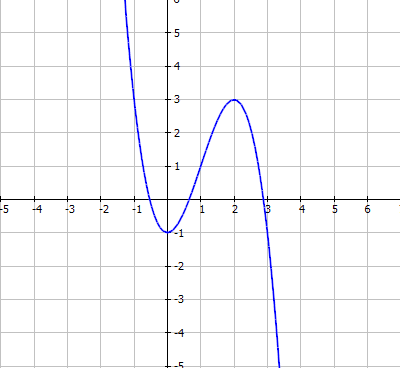
Sai lầm thường gặp khi giải toán và cách sửa

Hình ảnh được vẽ bởi phần mềm Function Grapher

Rồi chúng làm câu b như sau:

* Có $\frac{1}{3}x^3 - x^2 + m^2 = 0 \Leftrightarrow -x^3 + 3x^2 - 1 = 3m^2 - 1$ (*)

* Số nghiệm của phương trình (*) bằng số giao điểm của đồ thị $(C)$ và đường thẳng $\Delta: y=3m^2 - 1$ .

* Từ đồ thị suy ra, phương trình đã cho có 3 nghiệm phân biệt khi và chỉ khi

$-1<3m^2 - 1 < 3$

* Kết luận: $0 < m <\frac{2}{\sqrt{3}}$ là giá trị cần tìm.

Bạn có thấy không, sao chúng có thể mắc phải sai lầm “ngớ ngẩn” như thế được nhỉ? 😐

3. Hồn nhiên

Dạo lớp một vòng, rất nhiều cháu giải như vậy. Mình dừng lại ở một cháu trong số đó:

Mình hỏi: Đáp số của em, $m$ phải dương?
Nó trả lời ngon ơ: Vâng
Mình tiếp: Em thử lại với $m=-1$ xem?
Nó nháp: Với $m=-1 \Rightarrow \Delta: y = 2$
Mình tiếp: Ừ, khi đó $\Delta$ cắt $(C)$ tại mấy điểm?
Nó gãi đầu, gãi tai, cười xòa: 3 điểm 😀
Mình: “Cốc” vào đầu nó một cái! (Đáng đời “quân dốt … nhưng chưa nát”) 👿

4. Sai ở đâu?

Sai ở chỗ, cho rằng mệnh đề: “ $0 < m^2 < \frac{4}{3} \Leftrightarrow 0 < m < \frac{2}{\sqrt{3}}$ ” là đúng.

Nhưng thực ra mệnh đề này là SAI, ví dụ với $m=-1$ thì $0< (-1)^2 < \frac{4}{3}$ nhưng $0 < -1 < \frac{2}{\sqrt{3}}???$

5. Tại sao mắc sai lầm?

a. Áp dụng sai công thức khai căn

Rõ ràng, từ điều kiện $m^2 < \frac{4}{3}$ mà học sinh viết được $m < \frac{2}{\sqrt{3}}$ chứng tỏ học sinh đã thực hiện việc lấy căn hai vế:

$\sqrt{0} < \sqrt{m^2} < \sqrt{\frac{4}{3}}$

nhưng đến lúc khai căn thì lại sai:

$0 < m < \frac{2}{\sqrt{3}}$

Mà đúng ra phải là:

$0 < |m| < \frac{2}{\sqrt{3}}$

Như vậy, chính việc áp dụng sai công thức KHAI CĂN dẫn đến sai lầm. Thực tế dạy học cho thấy, dù đã học công thức khai căn $\sqrt{A^2}=|A|$ từ lớp dưới và được thực hành rất nhiều, nhưng học sinh vẫn rất “hay quên” và áp dụng sai công thức này.

b. Tại sao hay quên công thức?

Điều gì khiến học sinh “hay quên” công thức khai căn? Nguyên nhân nằm ở chính việc thực hành, áp dụng quá nhiều lần công thức khai căn với $A$ là các HẰNG SỐ nhưng lại rất ÍT KHI áp dụng với $A$ là những BIỂU THỨC đại số (có chứa chữ cái). Chẳng hạn:

$\sqrt{4}=\sqrt{2^2}=2$

$\sqrt{9}=\sqrt{3^2}=3$

$\sqrt{16}=\sqrt{4^2}=4$

…

Việc thường xuyên áp dụng công thức một cách “phiến diện” như thế hình thành ở học sinh một phản xạ di chuyển cả vào khi khai căn một BIỂU THỨC và sai lầm xảy ra:

$\sqrt{m^2}=m$ 😈 😈

6. Sửa như thế nào?

Qua phân tích trên, chúng ta có thể sửa như sau:

$0 < m^2 < \frac{4}{3} \Leftrightarrow 0 < |m| < \frac{2}{\sqrt{3}}$

$\Leftrightarrow \begin{cases}|m| > 0 \\ |m| < \frac{2}{\sqrt{3}}\end{cases} \Leftrightarrow \begin{cases}m \ne 0 \\ -\frac{2}{\sqrt{3}} < m < \frac{2}{\sqrt{3}}\end{cases} \Leftrightarrow m \in \left (-\frac{2}{\sqrt{3}};\frac{2}{\sqrt{3}}\right )\setminus\{0\}$

Do đó, đáp số của bài toán là: $m \in \left (-\frac{2}{\sqrt{3}};\frac{2}{\sqrt{3}}\right )\setminus\{0\}$

7. Bình luận

* Với học sinh khá, kiến thức chắc chắn thì bài toán này thật đơn giản và họ có thể trình bày rất ngắn gọn như sau:

$0 < m^2 < \frac{4}{3} \Leftrightarrow \begin{cases}m \ne 0 \\ -\frac{2}{\sqrt{3}} < m < \frac{2}{\sqrt{3}}\end{cases} \Leftrightarrow m \in \left (-\frac{2}{\sqrt{3}};\frac{2}{\sqrt{3}}\right )\setminus\{0\}$

* Khai căn một biểu thức đại số còn gặp ở rất nhiều bài toán khác và việc áp dụng sai công thức khai căn có thể dẫn đến nhiều sai lầm đáng tiếc. Chẳng hạn, một học sinh đã giải phương trình:

$\log_2{x^2} - 2\log_2{(3x+4)}=0$

như sau:

– Điều kiện: $\begin{cases}x^2 >0 \\ 3x+4>0\end{cases} \Leftrightarrow \begin{cases}x \ne 0 \\ x>-\frac{4}{3}\end{cases}$
– Phương trình đã cho tương đương với
$2\log_2{x} - 2\log_2{(3x+4)}=0 \Leftrightarrow \log_2{x} = \log_2{(3x+4)}$
$\Leftrightarrow x = 3x+4 \Leftrightarrow x = -2\ (ktm)$
– Kết luận: Phương trình vô nghiệm.

Trong khi, có thể thấy $x=-1$ là một nghiệm của phương trình. 😀

* Việc không giải được một bất phương trình đơn giản, kiểu như $x^2 < 4$ cho thấy học sinh đó không chỉ hổng kiến thức về khai căn mà còn hổng cả kiến thức giải bất phương trình bậc hai.

* Trong giảng dạy, thỉnh thoảng giáo viên nên tạo ra các tình huống khai căn với $A$ là bình phương của một biểu thức để học sinh được nhớ lại và áp dụng đúng công thức khai căn.

Oct 31, 2014Thapsang.vn

Viết bình luận

Xem tiếp bài có từ khóa

Mời bạn đón đọc các bài viết tiếp theo bằng cách đăng kí nhận bài viết mới qua email hoặc like fanpage Thapsang.vn để nhận được thông báo khi có cập nhật mới.

Xem tiếp← Một số sai lầm thường gặp khi giải toán và cách sửa (p4)