Nếu bạn đã từng học về lũy thừa, chắc hẳn bạn không quên định nghĩa sau đây trong sách giáo khoa toán:
[latexpage]
$a^0=1$ với $a\ne 0$
Khi học, bạn có thắc mắc rằng tại sao người ta lại định nghĩa như vậy không? Cụ thể, bạn có thắc mắc tại sao lũy thừa với số mũ 0 lại bằng 1 không? Nếu có thắc mắc thì bạn có kiến giải nào không? Sau đây là một kiến giải.
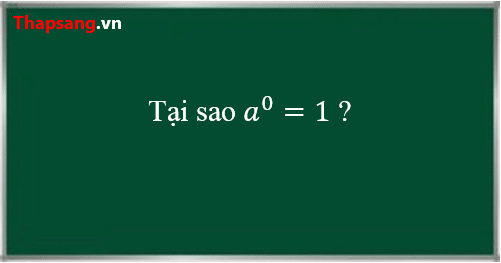
Tại sao lũy thừa với số mũ 0 lại bằng 1?
Câu trả lời là, với $a\ne 0$ mà $a^0 \ne 1$ thì sẽ có mâu thuẫn‼
Thật vậy, giả sử rằng $2^0=k$ và $k\ne1$ (*) khi đó một bài toán hết sức đơn giản sau đây sẽ có hai đáp số:
Tính giá trị của biểu thức
\[A=\frac{2}{2}\]
Vâng, thật là một bài toán hết sức đơn giản, đến mức quá tầm thường phải không, nhưng ta lại có thể giải nó theo 2 cách khác nhau với những đáp số khác nhau.
Cách 1: Thực hiện phép chia
Thực hiện một phép chia mà ai ai cũng biết. Thật là hiển nhiên, một số chia cho chính nó thì bằng 1 chứ còn bằng mấy? Vậy
\[A=1\ (1)\]
Nhưng mặt khác:
Cách 2: Áp dụng tính chất lũy thừa
Áp dụng tính chất của lũy thừa, ta có:
\[A=\frac{2^1}{2^1} = 2^{1-1}=2^0\]
Theo giả sử ở trên thì $2^0=k$ nên
\[A=k\ (2)\]
Từ (1)(2) ta có $k=1$, mẫu thuẫn với giả thiết (*): $k\ne 1$!! Sở dĩ có mâu thuẫn như thế là do ta đã giả sử $2^0$ khác 1.
Như vậy, với $a\ne 0$ thì $a^0=1$ và có thể nói định nghĩa này nhằm để hợp lý hóa hay có nguồn gốc từ phép toán $\frac{a^n}{a^n} =1$.
Đó là một cách kiến giải, bạn có kiến giải nào khác không? Nếu có, hãy chia sẻ nó vào hộp bình luận phía dưới nhé. Cảm ơn bạn!

