Một số sai lầm thường gặp khi giải toán và cách sửa (p3)

Khi mới làm quen với phương pháp ứng dụng đạo hàm để xét chiều biến thiên của hàm số, học sinh dễ mắc sai lầm khi áp dụng máy móc “quy tắc đan dấu”¹ để xét dấu đạo hàm. Dưới đây là một ví dụ.
[latexpage]

1. Đề bài
2. Sai ở đâu?
3. Tại sao sai?
4. Sửa như thế nào
5. Bình luận

1. Đề bài

Ví dụ: Xét chiều biến thiên của hàm số $y=x^4-6x^2+8x+1$

Lời giải

* Tập xác định: $D=\mathbb{R}$

* Ta có: $y’= 4x^3 – 12x + 8; y’=0 \Leftrightarrow x_1 = -2, x_2 = 1$ (Giải phương trình này là việc của … máy tính 😀 )

* Bảng biến thiên

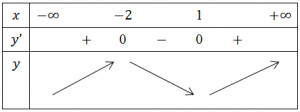
Từ bảng biến thiên, suy ra hàm số nghịch biến trên khoảng $(-2;1)$ và đồng biến trên các khoảng $(-\infty;-2)$ và $(1;+\infty)$

2. Sai lầm ở đâu?

Sai ở dấu của đạo hàm $y’$, trên khoảng $(-2;1)$ thì $y’$ phải mang dấu dương và trên khoảng $(-\infty;-2)$ thì $y’$ phải mang dấu âm. Không tin thì thử lại cho chắc 😀 , thay $x=0$ vào $y’$ thì $y'(0)=8>0$ do đó $y’>0$ trên khoảng $(-2;1)$.

3. Tại sao sai?

Đây là một bài toán đã có phương pháp giải và học sinh rất thành thục cách giải nên giải rất nhanh. Nhưng chính việc giải rất nhanh² này khiến học sinh không chú ý rằng phương trình $y’=0$ có nghiệm đặc biệt và cứ áp dụng “Quy tắc đan dấu” như các trường hợp thông thường nên điền sai dấu của $y’$.

Cụ thể, vì bậc của $y’$ là 3 trong khi phương trình $y’=0$ lại chỉ có 2 nghiệm nên chứng tỏ 1 trong hai nghiệm là nghiệm bội chẵn. Do đó dấu của $y’$ sẽ không tuân theo quy tắc đan dấu.

4. Sửa như thế nào?

Sau khi giải phương trình $y’=0$ có thể điền dấu cho $y’$ theo một trong các cách sau:

Cách 1: Xét dấu từng khoảng một, bằng cách chọn một giá trị phù hợp trong khoảng đó rồi tính $y’$ và kết luận dấu của $y’$ trong khoảng đó. (Cách này mất công bấm máy một tí, nhưng lợi hại nhất đấy )

Ví dụ với bài toán trên, trong khoảng $(-\infty; -2)$ ta chọn $x=-3$, trong khoảng $(-2;1)$ ta chọn $x=0$ và trong khoảng $(1;+\infty)$ ta chọn $x=2$

Cách 2: Đưa $y’$ về dạng tích từ đó đánh giá dấu của nó hoặc áp dụng chú ý về dấu cho nghiệm bội.

Ví dụ với bài toán trên, ta có thể đưa $y’$ về dạng tích: $y’=4(x-1)^2(x+2)$. Do $4(x-1)^2\ge 0,\forall x$ nên dấu của $y’$ là dấu của $x+2$, từ đó có lời giải đúng như sau

* Tập xác định: $D=\mathbb{R}$

* Ta có: $y’= 4x^3 – 12x + 8; y’=0 \Leftrightarrow x_1 = -2, x_2 = 1$

* Bảng biến thiên

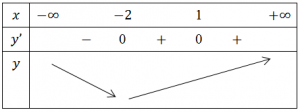
Từ bảng biến thiên, suy ra hàm số nghịch biến trên khoảng $(-\infty;-2)$ và đồng biến trên khoảng $(-2;+\infty)$

5. Bình luận

* Học sinh cũng có thể điền sai dấu của $y’$ như sau:

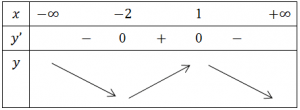
* Nếu gặp trường hợp $y’$ là đa thức và số nghiệm của phương trình $y’=0$ thấp hơn số bậc của $y’$ thì ta cần cẩn thận khi điền dấu của $y’$.

* Nếu $y’$ không là đa thức mà lại có chứa $x$ trong căn thức thì làm thế nào để xét dấu của $y’$? Chẳng hạn, xét chiều biến thiên của hàm số sau: $y=\sqrt{x+\sqrt{x^2-x+1}}$

1. Nếu bạn chưa biết quy tắc này thì bạn có thể Google để tìm hiểu [↩]
2. Đặc biệt, sẽ càng nhanh hơn nếu học sinh sử dụng máy tính để giải phương trình y’=0, rồi nhanh chóng điền dấu của y’ theo quy tắc đan dấu và lập bảng biến thiên [↩]