“Tính một logarit theo các logarit đã cho” là bài toán thường gặp với giáo viên và các bạn học sinh lớp 12, khi dạy và học về Logarit. Thực tế cho thấy, với bài dễ thì học sinh giải không khó khăn gì, nhưng với một bài toán khó hơn chút xíu thì nhiều bạn lại khá lúng túng. Sở dĩ có tình trạng như vậy là vì các bạn chưa nhìn ra bản chất của bài toán từ đó có một đường-lối chung để giải quyết các bài cùng loại. Bài viết này mình chia sẻ một đường-lối chung để giải quyết các bài toán loại này.
- Ví dụ 1: Tính logarit theo 1 logarit đã cho
- Ví dụ 2: Vẫn tính logarit theo 1 logarit đã cho 😀
- Bài toán tổng quát
- Ví dụ 3: Tính logarit theo 2 logarit đã cho
- Lưu ý dạy và học
Để tìm hiểu đường-lối đó ra sao, chúng ta bắt đầu với một ví dụ sau có trong SGK Giải tích 12.
1. Tính một logarit theo 1 logarit đã cho
theo Phân tích
* Vì hai logarit không cùng cơ số nên ta sẽ đổi cơ số của logarit cần tính về cơ số của logarit đã cho
* Do đó, bài toán trở thành
Tính 
theo 
* Nhận xét, vì hai logarit có cùng cơ số nên để tính logarit thứ nhất theo logarit thứ hai thì ta cần biểu diễn 
theo 
. Thật đơn giản, ta có 
, do đó:
* Để tập trung vào nội dung chính là tìm đường-lối chung, mình không trình bày lời giải của ví dụ này và các ví dụ dưới đây. Bạn tự trình bày nhé.
Bình luận
Bạn có thấy cách phân tích như thế dễ hiểu và tự nhiên không? Chỉ cần biểu diễn theo là chúng ta đã giải được bài toán một cách thật dễ dàng. Hãy sử dụng kinh nghiệm đó để giải tiếp một toán tương tự sau đây, xem sao:
2. Vẫn tính một logarit theo 1 logarit đã cho 😀
. Tính 
theo 
.Phân tích
* Với kinh nghiệm giải ví dụ 1 trên, nhận xét rằng hai logarit này cùng có cơ số là 
nên một cách tự nhiên ta nghĩ đến việc biểu diễn 
theo 
* Ồ, bạn thấy ngay! Làm sao có thể biểu diễn theo được? Chúng là hai số nguyên-tố-cùng-nhau mà2. Vậy, nếu không biểu diễn được theo thì làm sao tính được theo 
đây?
* Nhưng rõ ràng, ở ví dụ 1 chỉ cần biểu diễn theo là ta có thể giải quyết bài toán thật “ngon lành” mà. Không nhẽ vì ta đã giải ví dụ 1 một cách dễ dàng quá nên chưa hiểu hết bản chất của cách giải chăng? Thử nghiên cứu lại cách giải ở ví dụ 1 xem sao? Ta đã làm gì:
– Vì cần biểu diễn theo nên ta viết
– Sau đó áp dụng phép toán logarit của một thương, ta có: 
– Tiếp theo, vì 
nên áp dụng phép toán logarit của một lũy thừa có cùng cơ số, ta có:
* Ồ, phải rồi. Sở dĩ việc biểu diễn theo giúp tính được theo 
là vì ta tính được 
. Việc tính được là vì 
là lũy thừa có cơ số bằng với cơ số của logarit (cơ số 
). Như vậy, bản chất của cách giải trên không chỉ có mỗi việc biểu diễn theo mà phải hiểu là đầy đủ là: “Biểu diễn theo tích hoặc thương các lũy thừa của và của – cơ số của logarit.”3
* Hãy vận dụng hiểu biết mới này cho ví dụ trên. Để tính theo , ta cần biểu diễn theo tích hoặc thương của các lũy thừa nào? Đó là lũy thừa của cơ số và đối của logarit đã cho: và . Ta có:
* Do đó, bài toán được giải quyết:
Kết luận
Muốn tính một logarit theo một logarit đã cho cùng cơ số ta biểu diễn đối số của logarit cần tính thành tích hoặc thương các lũy thừa của cơ số và đối số của logarit đã cho. Đó chính là nội dung của bài toán tổng quát dưới đây.
3. Bài toán tổng quát
với 
và 
. Tính 
theo 
.Giải
* Giả sử tồn tại hai số 
sao cho 
* Khi đó ta có:
Nhận xét:
– Nếu không tồn tại hai số 
thỏa mãn thì rõ ràng bài toán không có đáp số!
– Nếu tồn tại 2 số sao cho 
thì tính tương tự.
– Trong thực hành, mấu chốt là tìm được hai số . Đòi hỏi bạn phải khéo léo biến đổi, thực hiện các phép toán số học và lũy thừa.
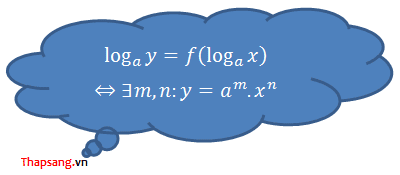
Cách tính một logarit theo một logarit cùng cơ số cho đã cho.
Vậy bạn nhớ nhé, cứ “Biểu diễn đối số của logarit cần tính thành tích/thương các lũy thừa của cơ số và đối số của logarit đã cho” là bài toán được giải quyết. Giờ chúng ta sẽ vận định-hướng này cho ví dụ dưới đây.
4. Tính một logarit theo 2 logarit đã cho
. Tính 
theo 
.Phân tích
* Vì logarit cần tính không cùng cơ số với hai logarit đã cho nên trước tiên ta cần đổi về cùng cơ số 
:
* Dễ thấy rằng 
nên 
* Giờ ta tiếp tính 
theo các logarit 
và 
. Muốn vậy, ta chỉ cần biểu diễn 
thành tích/thương các lũy thừa của 
và là xong. Ta có:
Suy ra 
* Vậy 
5. Lưu ý dạy và học
* SGK đã trình bày lời giải ví dụ 1 ở trên, như sau:
Ta có
suy ra
Vậy
Bạn có thấy cách trình bày dễ hiểu và tự nhiên không? Mình nghĩ cách trình bày như vậy rất không tự nhiên, khó hiểu với những bạn mới bắt đầu học về logarit và do đó nó không giúp ích gì nhiều cho các bạn tự học.
* Hãy dùng bí-quyết trên để giải quyết các bài toán tương tự mà bạn gặp. Nếu bạn gặp một bài toán loại này mà bí-quyết trên không giúp bạn giải được nó thì hãy gõ nó hộp bình luận dưới đây và chúng ta cùng “xử-lý” nó. 😀
Xem tiếp phần 2: Cách tính một logarit theo các logarit đã cho (Phần 2)
- SGK Giải tích 12, NXB Giáo dục, 2008, trang 66, ví dụ 7 [↩]
- Trong toán học, các số nguyên a và b được gọi là nguyên tố cùng nhau nếu chúng có Ước số chung lớn nhất là 1. Ví dụ 6 và 35 là nguyên tố cùng nhau vì chúng có ước chung lớn nhất là 1, nhưng 6 và 27 không nguyên tố cùng nhau vì chúng có Ước chung lớn nhất là 3 [↩]
- Bạn có thể thắc mắc, tại sao lại là tích hoặc thương? Là tổng hay hiệu thì sao? Nếu bạn tự đặt được câu hỏi đó thì chúc mừng bạn nhé, bạn có tư duy phê phán rất tốt. Và thách thức của bạn là “Sao bạn không tự tìm câu trả lời nhỉ?” Nếu bí quá thì cứ gõ đề nghị giải thích vào hộp bình luận ở phía dưới [↩]
