Home » Dạy và học toán » Cách xác định hướng của tích vectơ (Tích có hướng)

Cách xác định hướng của tích vectơ (Tích có hướng)

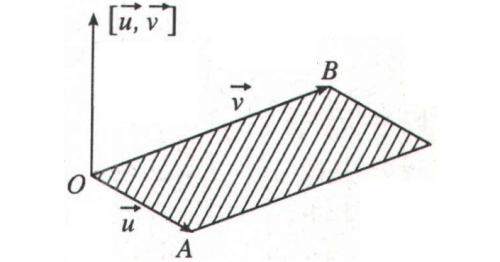
Là học sinh lớp 12, sau khi học xong định nghĩa về tích có hướng (hay tích vectơ) của hai vectơ \vec{u} và \vec{v} và nhìn thấy hình vẽ sau trong SGK, bạn có “nảy” ra một câu hỏi nào không?

Một hình vẽ trong SGK Hình học 12 Nâng cao

Một hình vẽ trong SGK Hình học 12 Nâng cao)

Câu hỏi của bạn là gì? Nếu câu hỏi của bạn là “Tại sao SGK lại vẽ hướng của vectơ [\vec{u},\vec{v}] là hướng lên mà không phải là hướng xuống?” và bạn đang tìm kiếm câu trả lời? Chào mừng bạn, bạn tìm đúng địa chỉ rồi đấy, bài viết này chúng ta sẽ trả lời câu hỏi đó.

info

LƯU Ý: Bài viết mang tính chuyên sâu và khá dài, nếu bạn thật sự muốn tìm hiểu và mở rộng kiến thức của mình thì bạn nên cân nhắc thời gian để đọc toàn bộ bài viết. Nếu kiến thức của bạn tốt và bạn có ít thời gian thì có thể bắt đầu đọc từ mục 4.
  1. Tích có hướng của hai vectơ
  2. Vấn đề
  3. Một định nghĩa khác
  4. Tam diện thuận
  5. Thực hành một chút
  6. Còn thắc mắc?
  7. Tài liệu tham khảo

Trước tiên chúng ta nhắc lại tích có hướng của hai vectơ là gì và một số tính chất cơ bản của nó.

1. Tích có hướng của hai vectơ

Định nghĩa

Theo SGK Hình học 121 thì tích có hướng của hai vectơ định nghĩa theo biểu thức tọa độ như sau:

Trong không gian tọa độ Oxyz, tích có hướng (hay tích vectơ) của hai vectơ \vec{a}=(a_1;a_2;a_3) và \vec{b}=(b_1;b_2;b_3) là một vectơ được kí hiệu là [\vec{a},\vec{b}] (hoặc \vec{a} \wedge \vec{b}) và có tọa độ được xác định như sau:

    \[[\vec{a},\vec{b}]=\left (\begin{vmatrix} a_2 & a_3 \\ b_2 & b_3 \end{vmatrix};\begin{vmatrix} a_3 & a_1 \\ b_3 & b_1 \end{vmatrix};\begin{vmatrix} a_1 & a_2 \\ b_1 & b_2 \end{vmatrix}\right )\]

    \[=(a_2b_3 - a_3b_2; a_3b_1 - a_1b_3; a_1b_2 - a_2b_1)\]

Tính chất

Tích có hướng của hai vectơ \vec{a} và \vec{b} có một số tính chất quan trọng sau:2

a) Vectơ [\vec{a},\vec{b}] vuông góc đồng thời cả hai vectơ \vec{a} và \vec{b}.

b) |[\vec{a},\vec{b}]| = |\vec{a}|.|\vec{b}|.\sin{(\vec{a},\vec{b})}

c) [\vec{a},\vec{b}] = - [\vec{b},\vec{a}]

Tiếp theo, chúng ta sẽ phát triển câu hỏi ban đầu thành một bài toán và cố gắng sử dụng hiểu biết trên để giải quyết nó.

2. Vấn đề

Bài toán

Trong không gian Oxyz, cho hai vectơ \vec{u} và \vec{v} không cùng phương3 và có cùng điểm đầu O, như hình vẽ. Hãy xác định hướng của vectơ [\vec{u},\vec{v}], biết [\vec{u},\vec{v}] có điểm đầu là O.

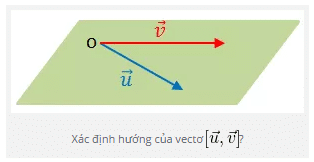
Phân tích

* Từ tính chất (a) suy ra vectơ [\vec{u},\vec{v}] vuông góc với mặt phẳng (P) chứa hai vectơ \vec{u} và \vec{v}.

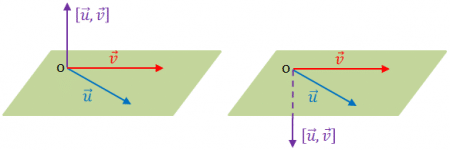
* Cũng dễ thấy rằng, có hai loại vectơ cùng vuông góc với mặt phẳng (P) nhưng có hướng ngược nhau, loại có hướng “lên trên” và loại có hướng “xuống dưới”.

* Trong khi theo định nghĩa thì vectơ [\vec{u},\vec{v}] là duy nhất, do đó vấn đề là vectơ [\vec{u},\vec{v}] thuộc loại nào? Loại có hướng lên trên hay có hướng xuống dưới?

Hướng lên hay hướng xuống?

Hướng lên hay hướng xuống?

Còn thiếu gì chăng?

Nhận xét rằng, trong các kiến thức trên (định nghĩa và các tính chất của tích có hướng) không có kiến thức nào đề cập hay gợi ý cho ta cách xác định “hướng” của vectơ [\vec{u},\vec{v}] cả, chúng chỉ đủ để giúp chúng ta xác định được phương (tính chất a) và độ dài (tính chất b) của vectơ [\vec{u},\vec{v}] mà thôi.

Nếu đọc kĩ SGK Hình học 12, bạn sẽ thấy rằng SGK không hề đề cập đến vấn đề “hướng” của vectơ [\vec{u},\vec{v}]. Vậy làm thế nào để xác định hướng của vectơ [\vec{u},\vec{v}] đây? Câu trả lời nằm trong một định nghĩa khác về tích có hướng của hai vectơ, một định nghĩa thường gặp trong môn Vật lý ở … bậc Đại học. Hiển nhiên, định nghĩa này không có trong SGK Hình học 12. 😀 (Ừm, mình muốn nói là Kiến thức trong SGK Hình học 12 là không đủ)

3. Một định nghĩa khác

Trong Vật lý, người ta thường định nghĩa tích có hướng một cách hình học4 như sau:

Tích có hướng của hai vectơ \vec{a} và \vec{b} là một vectơ \vec{c} được kí hiệu là \vec{a} \wedge \vec{b} hoặc [\vec{a},\vec{b}] và xác định như sau:

i) \vec{c} vuông góc với cả \vec{a} và \vec{b}

ii) |\vec{c}| = |\vec{a}|.|\vec{b}|.\sin{(\vec{a},\vec{b})}

iii) Khi \vec{a}, \vec{b} không cùng phương và ba vectơ \vec{a}, \vec{b}, \vec{c} cùng có chung điểm đầu là O thì theo thứ tự đó chúng tạo thành một tam diện thuận.

Bạn chú ý, trong định nghĩa trên, điều kiện (i) xác định phương của vectơ [\vec{a},\vec{b}], điều kiện (ii) xác định độ dài của vectơ [\vec{a},\vec{b}] còn điều kiện (iii) xác định hướng của vectơ [\vec{a},\vec{b}]. Từ định nghĩa này, người ta suy ra được biểu thức tọa độ của tích có hướng như trình bày ở mục 1.

Bạn sẽ lại thắc mắc, “nhưng cụm từ tam diện thuận trong điều kiện (iii) là gì?”.

4. Tam diện thuận

Quy tắc

Có thể phát biểu quy tắc tam diện thuận như sau:

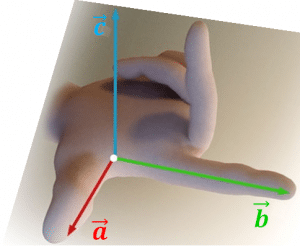
Ba vectơ \vec{a}, \vec{b}, \vec{c} theo thứ tự đó được gọi là tạo thành một tam diện thuận, nếu đặt bàn tay phải của bạn sao cho ngón cái là vectơ \vec{a}, ngón trỏ là vectơ \vec{b} thì ngón giữa (vuông góc với lòng bàn tay) là vectơ \vec{c}

Xac-dinh-huong-tich-vecto-bang-Quy-tac-ban-tay-phai

Tam diện thuận và Hệ tọa độ Oxyz

Trên thực tế, bạn đã tiếp cận quy tắc tam diện thuận này ngay từ khi học về hệ tọa độ Oxyz. Thật vậy, trên hệ tọa độ Oxyz, với ba vectơ đơn vị \vec{i},\vec{j},\vec{k} lần lượt nằm trên ba trục Ox, Oy, Oz thì bộ 3 các vectơ có thứ tự: (\vec{i},\vec{j},\vec{k}), (\vec{j},\vec{k},\vec{i}), (\vec{k},\vec{i},\vec{j}) lập thành các tam diện thuận.

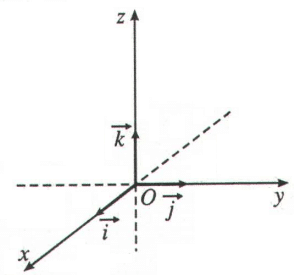
Hệ trục tọa độ Oxyz (Hình chụp SGK Hình học 12 Nâng cao)

Hệ trục tọa độ Oxyz (Hình chụp SGK Hình học 12 Nâng cao)

Để ý rằng, nếu áp dụng định nghĩa hình học về tích có hướng thì ta sẽ thu được các công thức: (Trong SGK Hình học 12, các công thức này được chứng minh bằng biểu thức tọa độ)

    \[[\vec{i},\vec{j}]=\vec{k}, [\vec{j},\vec{k}]=\vec{i},[\vec{k},\vec{i}]=\vec{j}\]

Câu trả lời cho bài toán

Quay trở lại với bài toán trên, áp dụng quy tắc tam diện thuận chúng ta có ngay đáp số: Vectơ [\vec{u},\vec{v}] có hướng lên trên. Tương tự như vậy, bạn đã hiểu tại sao vectơ [\vec{u},\vec{v}] trong hình vẽ của SGK Hình học 12 (Hình 1) lại có hướng lên rồi chứ?

5. Thực hành

Khi dùng bàn tay phải để xác định hướng của tích vectơ [\vec{x}, \vec{y}], kinh nghiệm hữu ích cho những bạn mới bắt đầu là: 1) trước tiên bạn nên đặt bàn tay phải của bạn song song với mặt phẳng chứa hai vectơ \vec{x} và \vec{y}; 2) sau đó rồi mới lựa bàn tay sao cho ngón cái và ngón trỏ lần lượt cùng hướng với các vectơ \vec{x} và \vec{y}; 3) cuối cùng, để ngón giữa vuông với bàn tay thì hướng của ngón giữa là hướng của vectơ [\vec{x}, \vec{y}].

“Học đi đôi với hành”, hãy thực hành ngay và luôn 😀

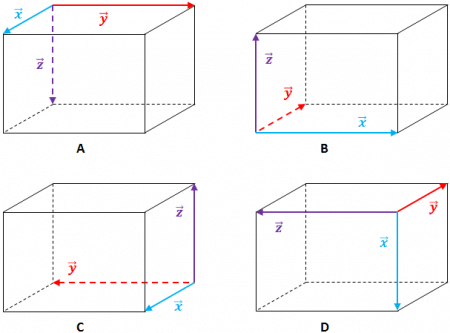
Cho ba vectơ \vec{x},\vec{y},\vec{z} nằm trên các cạnh của một hình hộp chữ nhật và \vec{z}=[\vec{x},\vec{y}]. Trong các hình vẽ sau, hình vẽ nào diễn tả đúng hướng của vectơ \vec{z}:

thuc-hanh-quy-tac-tam-dien-thuan

Hãy gõ đáp án của bạn vào hộp bình luận phía dưới nhé.

6. Còn thắc mắc?

* Có thể bạn sẽ thắc mắc: định nghĩa hình học của tích có hướng của hai vectơ cho phép xác định được độ dài và cả hướng của tích vectơ, nó đầy đủ hơn định nghĩa theo biểu thức tọa độ, vậy tại sao SGK không dùng định nghĩa này?” Vấn đề là ở chỗ, việc xây dựng biểu thức tọa độ này là khó đối với học sinh nên SGK đã không trình bày định nghĩa này mà lấy luôn biểu thức tọa độ làm định nghĩa của tích có hướng.5

* Bạn cũng có thể thắc mắc: Liệu có thể phát biểu/thể hiện quy tắc tam diện thuận theo một cách khác được không? Chẳng hạn, có thể dùng bàn tay trái được không? Một câu hỏi tốt, nếu bạn có khả năng đặt câu hỏi thì chắc chắn bạn sẽ có khả năng tìm câu trả lời. Hãy thử xem và đừng quên “quyền trợ giúp”: Google nhé! 😀

* Bạn vẫn còn thắc mắc khác? Hãy gõ nó vào hộp bình luận phía dưới nhé.

7. Tài liệu tham khảo

* SGK Hình học 12 (Cơ bản, Nâng cao), NXB Giáo dục, 2008

* SGV Hình học 12 Nâng cao, NXB Giáo dục, 2008

* Định nghĩa Tích có hướng (tích vectơ) của hai vectơ: Đại học Cần Thơ

* Tích vectơ: Wikipedia

* Xác định hướng của tích vectơ bằng quy tắc bàn tay phải: Wikipedia

* Tích có hướng là gì: Wikibooks

“ Học từ hôm qua, sống cho ngày hôm nay và hy vọng cho ngày mai. Điều quan trọng là không ngừng đặt câu hỏi. ”
— Albert Einstein


Thapsang.vn
Bài hay?Viết bình luận

Share
Xem tiếp bài có từ khóa

Mời bạn đón đọc các bài viết tiếp theo bằng cách đăng kí nhận bài viết mới qua email hoặc like fanpage Thapsang.vn để nhận được thông báo khi có cập nhật mới.

Có thể bạn muốn xem

Từ trục tung, trục hoành đến tung và hoành
Cách chứng minh bài toán hình học phẳng
Cách phân tích bài toán rút gọn biểu thức
Tại sao nên vẽ đường cao của hình chóp theo phương thẳng đứng?
  1. Cả SGK Nâng cao và Cơ bản [↩]
  2. Theo SGK Hình học 12 Nâng cao [↩]
  3. Chú ý rằng, hai vectơ không cùng phương thì hai vectơ đó đều khác vectơ không [↩]
  4. Định nghĩa dạng này cũng được nhắc đến trong SGV Hình học 12 Nâng cao và bạn sẽ còn gặp lại nó ở môn Vật lý trên bậc Đại học [↩]
  5. SGV Hình học 12 Nâng cao [↩]
Gộp các đối tượng thành một nhóm trong MS Word 2010Giảm dung lượng file video AVI
Comments: 39
  1. vodanhtienboi
    9 years ago

    rất hay bạn!

    ReplyCancel
  2. Đợi Anh Giàu Nhé
    9 years ago

    hay quá

    ReplyCancel
  3. Nguyễn Đình Khoa
    9 years ago

    Thầy viết hay lắm

    ReplyCancel
  4. Lý Hoàng Trí Nhân
    9 years ago

    Em rất cảm ơn bài viết của thầy ạ, nhờ nó mà em hiểu được ý nghĩa của khái niệm tích có hướng hai vectơ.
    Phần áp dụng là câu B đúng.

    ReplyCancel
  5. 9 years ago

    Cho em hỏi bàn tay phải nên để ngửa hay để úp

    ReplyCancel
    • Ánh
      2 years ago

      lúc úp lúc ngửa bạn ơi, cứ ngón cái theo vt x và ngón trỏ theo vt y là nó ra thui nhé.

      ReplyCancel
  6. 9 years ago

    Em để thế nào cũng được, miễn là đúng thứ tự như Quy tắc nêu trong bài.

    ReplyCancel
  7. 9 years ago

    B :v

    ReplyCancel
  8. 9 years ago

    Có thể phát biểu ba vectơ x⃗ ,y⃗ ,z⃗ theo thứ tự tạo thành tam diện thuận như sau: Nếu nhìn ngược hướng véc tơ z⃗ , ta phải quay véc tơ x⃗ góc 90 độ ngược chiều kim đồng hồ để được x⃗ cùng hướng với y⃗ .

    ReplyCancel
    • 9 years ago

      Cảm ơn bạn!

      ReplyCancel
    • BằngLưu
      8 years ago

      Đúng rồi, hình dung 2 véc tơ x, y cùng điểm gốc trước mặt và hướng về phía mình, nếu x trỏ sang trái, y trỏ sang phải thì z trỏ lên trên; ngược lại thì z trỏ xuống dưới.

      ReplyCancel
  9. Ngọc Hổ
    9 years ago

    Đặc bàn tay phai theo hướng dẫn thì hình như A, B đúng. Còn C, D thì sai.

    ReplyCancel
  10. hà nguyễn
    9 years ago

    thầy cho em hỏi với, nếu 2 véc tơ a (a1, a2,0) và vec tơ b (b1,b2,0) tức là trên mặt phẳng oxy, góc giữa vec tơ a và vecto b là alpha (quay từ vt a sang vt b), góc alpha trong khoảng từ 0 đến 180 độ
    nếu em dùng tích hữu hướng cho vec tơ c(0,0,c1), nếu c1>0 thì alpha 0 thì alpha >0 (góc alpha quy ước nếu cùng chiều kim đồng hồ là dấu -, ngược chiều kim đồng hồ là dấu +
    là luôn đúng phải không ạ, em đang tự mày mò học máy kinh vĩ, em cảm ơn thầy

    ReplyCancel
  11. hà nguyễn
    9 years ago

    em viết lại ý là a^b=c, c3>0 thì alpha <0
    c30

    ReplyCancel
  12. 9 years ago

    hay

    ReplyCancel
  13. 8 years ago

    B

    ReplyCancel
  14. 8 years ago

    tai sao n=(a.b) mak ko phải là n=(b.a)

    ReplyCancel
  15. 8 years ago

    Bạn có thể đặt câu hỏi rõ ràng hơn?

    ReplyCancel
  16. 8 years ago

    Bạn có thể đặt câu hỏi rõ ràng hơn?

    ReplyCancel
  17. 8 years ago

    B

    ReplyCancel
  18. Nguyễn Thị Giàu
    8 years ago

    B phải ko nhỉ

    ReplyCancel
  19. 8 years ago

    Rất hay

    ReplyCancel
  20. Nguyễn Thị Vân Anh
    8 years ago

    Em cám ơn thầy ạ, phần hướng dẫn của thầy rất có ích với em ạ 😀

    ReplyCancel
  21. 8 years ago

    trắng như cc vừa xem cái biến mất cái mả bố nhà mày tau ức chế lắm rồi đó nha

    ReplyCancel
  22. 8 years ago

    Hãy giữ lịch sự khi bình luận. Đề nghị bạn sửa một số từ thiếu lịch sự trong bình luận của bạn, nếu không 24h sau tôi sẽ phải xóa bình luận của bạn.

    ReplyCancel
  23. Viethvktqs
    8 years ago

    Nếu vector có 4 chiều thì sao ạ

    ReplyCancel
    • 8 years ago

      Một câu hỏi hay, mình chưa nghĩ đến. Cảm ơn chia sẻ của bạn, mình sẽ suy nghĩ và trao đổi sau nhé. 🙂

      ReplyCancel
  24. 7 years ago

    Thầy ơi! cho e hoi cach tinh khoang cach giua hai vector thi lam the nao ạ!!

    ReplyCancel
    • 7 years ago

      Thầy nghĩ không có công thức đó, em kiểm tra lại câu hỏi xem có nhầm lẫn gì không?

      ReplyCancel
  25. lê hưng
    7 years ago

    đáp án b phải ko

    ReplyCancel
  26. 7 years ago

    ngón Cái bắt buột là vecto x, ngón Trỏ là vecto y, hay là sao ak, đảo lộn chúng được không ak

    ReplyCancel
  27. Ngọc
    4 years ago

    A,D

    ReplyCancel
  28. Nguyễn Thị Hiền
    3 years ago

    B

    ReplyCancel
  29. son
    9 months ago

    Quy tắc bàn tay phải (Right-Hand Rule):
    Để xác định hướng của tích vectơ, ta sử dụng quy tắc bàn tay phải:
    Giữ bàn tay phải với lòng bàn tay hướng lên.
    Nếu ngón tay cái trỏ theo hướng vectơ a, ngón áp út trỏ theo hướng vectơ b, thì ngón giữa sẽ trỏ theo hướng của tích vectơ a × b.
    Ứng dụng:
    Tích có hướng giúp xác định hướng của quỹ đạo quay, lực từ, và nhiều hiện tượng khác trong vật lý.
    Nó cũng được sử dụng trong tính toán vector và động học.
    Vậy làm theo quy tắc bàn tay phải, bạn có thể xác định hướng của tích vectơ một cách chính xác!

    ReplyCancel
  30. Nguyen
    8 months ago

    B

    ReplyCancel

Trả lời

Thapsang.vn

Chào bạn, Thapsang.vn – nơi chia sẻ các thông tin, kiến thức bổ ích về giáo dục và công nghệ, hoạt động từ 10/2012 đến nay. Hi vọng bài viết này có ích cho bạn và mong nhận được nhiều phản hồi của bạn. Cảm ơn bạn đã đọc bài viết!

9 years ago 39 Comments Dạy và học toán, , , 118,691