Vận dụng định lý Côsin một cách thành thạo là yêu cầu bắt buộc với hầu hết các học sinh THPT. Dưới đây mình trình bày định lý này cùng hệ quả của nó và kinh nghiệm vận dụng chúng.
1. Định lý Côsin
![]()
![]()
Định lý có một ý nghĩa rất quan trọng:
“Trong một tam giác, ta luôn tính được cạnh thứ ba nếu biết hai cạnh và góc xen giữa“
Từ định lý trên, ta dễ dàng suy ra hệ quả sau
2. Hệ quả
![]()
![]()
Hệ quả này có một ý nghĩa quan trọng:
“Trong một tam giác, ta luôn tính được các góc nếu biết 3 cạnh.“
3. Vận dụng
Ví dụ. Cho tam giác ![]() , có
, có ![]() và
và ![]() là trung điểm của
là trung điểm của ![]() . Tính độ dài đường trung tuyến
. Tính độ dài đường trung tuyến ![]() theo
theo ![]() và
và ![]() .
.
Phân tích
* Bài toán yêu cầu chúng ta tính độ dài một đoạn thẳng AM, mà nguyên tắc hay dùng để tính đoạn thẳng là xem nó là một cạnh của một giác nào đó.
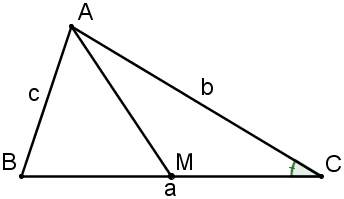
* Theo đề bài, chúng ta có 2 lựa chọn, hoặc xem AM là cạnh của tam giác ABM hoặc là cạnh của tam giác ACM. Nhận thấy, vai trò của hai tam giác này là ngang nhau nên ta chọn tam giác nào cũng được. Mình chọn tam giác ACM. Lý do là vì Google khuyên vậy, 😯 nó bảo có khoảng 38.200.000 kết quả cho từ khóa ACM trong khi chỉ có khoảng 17.800.000 kết quả cho từ khóa ABM 
* Xét tam giác ACM, theo nguyên tắc chung, để tính cạnh AM ta cần biết hai cạnh còn lại là AC, CM và góc xen giữa hai cạnh đó là C. Dễ thấy AC=b theo giả thiết, còn ![]() do M là trung điểm của BC, nhưng thật đáng tiếc là ta chưa biết góc C! Như vậy, nếu tính được góc C thì AM sẽ tính được nhờ định lý Côsin.
do M là trung điểm của BC, nhưng thật đáng tiếc là ta chưa biết góc C! Như vậy, nếu tính được góc C thì AM sẽ tính được nhờ định lý Côsin.
![]()
* Nhận xét rằng, muốn tính góc trong tam giác ta cần biết ba cạnh của tam giác đó. Do đó, không thể xét tam giác ACM để tính góc C được, vì tam giác này đang còn thiếu cạnh AM mà ta cần tính.
* Nhưng, dễ thấy rằng góc C của tam giác ACM cũng là góc C của tam giác ABC. Trong khi tam giác ABC đã có cả 3 cạnh, vậy áp dụng hệ quả của định lý Côsin ta sẽ tính được góc C.
![]()
* Thay (2) vào (1), rồi rút gọn ta có kết quả
![]()
* Về lời giải, giống như nhiều bài viết khác, câu của mình vẫn là “Bạn tự làm nhé!” 😀
4. Bình luận
* Ta đã xây dựng được công thức đường trung tuyến của tam giác theo ba cạnh, là nhờ dựa vào hai luận điểm cơ bản “Muốn tính một cạnh, thì cần biết hai cạnh còn lại và góc xen giữa”, “Muốn tính một góc, thì cần biết cạnh”. Đó cũng chính là hai ý nghĩa quan trọng của định lý Côsin và hệ quả của nó.
* Hiển nhiên, một bài toán có thể giải bằng nhiều cách! Vậy bạn có cách giải nào khác mà không dùng đến định lý Côsin và hệ quả của nó thì mách mình nhé. Hộp bình luận luôn ở dưới cuối bài viết này, mời bạn!


