Home » Làm toán » Hỏi đáp: Cách tính một logarit theo các logarit đã cho

Hỏi đáp: Cách tính một logarit theo các logarit đã cho

Bạn đang xem phần 3 / 3 của series Cách tính logarit.

Trang này dành giải đáp thắc mắc của các bạn về cách tính một logarit theo logarit đã cho. Ở các bài viết:

Các câu hỏi:

  1. Q1: Bởi bạn tiên-học-toán
  2. Q2: Bởi bạn Long Phạm
  3. Q3: Bởi bạn Bảo trần
  4. Q4: Bởi bạn Khanhnguyen
  5. Q5: Bởi bạn Hddh

Q1: Bởi bạn tiên học toán

Câu hỏi: Cho a=\log_{5}{18}; b=\log_{5}{60}. Hãy biểu diễn \log_{3}{2} theo a và b.

Nguồn: Bình luận trên Thapsang.vn tại đây

Đáp:

* \log_{5}{60}=\log_{5}{(5.12)}=1+\log_{5}{12}\Rightarrow \log_{5}{12}=b-1

* \log_{3}{2}=\frac{\log_5 2}{\log_5 3}

* Tính \log_5 2 theo \log_{5}{18},\log_{5}{12}

– Giả sử tồn tại ba số m,n,p sao cho 2=5^m.18^n.12^p\Leftrightarrow 2=2^{n+2p}.3^{2n+p}.5^m

– Vì 2, 3 và 5 là các số nguyên tố cùng nhau nên

\begin{cases}n+2p=1 \\ 2n+p=0 \\ m =0\end{cases}\Leftrightarrow \begin{cases}m=0\\n=-\frac{1}{3}\\ p=\frac{2}{3}\end{cases}

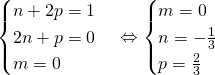
– Do đó \log_{5}{2}=\log_5{(18^\frac{-1}{3}.12^\frac{2}{3})}=-\frac{1}{3}\log_{5}{18}+\frac{2}{3}\log_{5}{12}=-\frac{1}{3}a+\frac{2}{3}b-\frac{2}{3}

* Tương tự, tính \log_5 3 theo \log_{5}{18},\log_{5}{12}. Bạn \log_5{3}=\frac{2}{3}a-\frac{1}{3}b+\frac{2}{3}

* Kết quả: \log_3 2 = \frac{-a+2b-2}{2a-b+2}

Q2: Bởi bạn Long Phạm

Câu hỏi: Cho a=\log_{12}{2}. Tính \log_{27}{12} theo a

Nguồn: Bình luận trên Thapsang.vn tại đây

Đáp:

* Ta có \log_{27}{12}=\frac{1}{\log_{12}{27}}=\frac{1}{3\log_{12}{3}}

* Bài toán trở thành: Tính \log_{12}{3} theo \log_{12}{2}

– Giả sử tồn tại hai số m,n sao cho 3=12^m.2^n \Leftrightarrow 3=3^m.2^{n+2m}

– Vì 2 và 3 là các số nguyên tố cùng nhau nên

\begin{cases}m=1 \\ n+2m = 0\end{cases}\Leftrightarrow \begin{cases}m=1 \\ n = -2\end{cases}

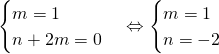
– Do đó \log_{12}{3}=\log_{12}{(12^1.2^{-2})}=1-2\log_{12}{2}=1-2a

* Vậy \log_{27}{12}=\frac{1}{3(1-2a)}

Bình luận: Bạn có thể tính \log_{12}{3} theo \log_{12}{2} nhanh hơn, như sau

\log_{12}{3}=\log_{12}{\frac{12}{4}}=\log_{12}{12}-\log_{12}{4}=1-2\log_{12}{2}=1-2a

Q3: Bởi bạn Bảo Trần

Câu hỏi: Tính \log_{49}{16} theo a=\log_{14}{28}.

Nguồn: Bình luận trên Thapsang.vn tại đây

Đáp:

* Trước tiên ta sẽ đơn giản các logarit và cố gắng đưa chúng về cùng một cơ số, ta có

\log_{49}{16} = 2\log_{7}{2}, \log_{14}{28}=\log_{14}{2}+1

* Nhận thấy hai logarit \log_{7}{2} và \log_{14}{2} đều có thể đưa về cơ số 2, thật vậy

\log_{7}{2} = \frac{1}{\log_{2}{7}} và \log_{14}{2}=\frac{1}{\log_{2}{14}} = \frac{1}{1+\log_{2}{7}}

* Từ đó suy ra

\log_{49}{16}=\frac{2}{\log_{2}{7}} và a = 1+ \frac{1}{1+\log_{2}{7}}\Leftrightarrow \log_2{7}=\frac{2-a}{a-1}

Do đó, \log_{49}{16}= \frac{2(a-1)}{2-a}



Thapsang.vn
Bài hay?Viết bình luận

Share
Xem tiếp bài có từ khóa

Mời bạn đón đọc các bài viết tiếp theo bằng cách đăng kí nhận bài viết mới qua email hoặc like fanpage Thapsang.vn để nhận được thông báo khi có cập nhật mới.
Xem tiếp← Cách tính một logarit theo các logarit đã cho (Phần 2)
Cách nhẩm nghiệm phương trình bậc haiSử dụng phần mềm Microsoft Mathematics kết hợp với MS Word 2010
Comments: 7
  1. 5 years ago

    Cảm ơn mìh đã hjểu đc cách này. Mong b có nhju bài viết tương tự

    ReplyCancel
  2. 4 years ago

    Hay nhỉ

    ReplyCancel
  3. 4 years ago

    rất hay

    ReplyCancel
  4. 2 years ago

    cho log15(3)=a.tínhlog25(15) theo a

    ReplyCancel
    • 2 years ago

      Em tham khảo:

      \[\log_{15}{3}=\frac{1}{\log_{3}{15}}=\frac{1}{1+\log_{3}{5}}\]

      \[\log_{25}{15}=\frac{\log_{3}{15}}{2\log_{3}{5}}=\frac{\frac{1}{a}}{2(\frac{1}{a}-1)}=\frac{1}{2(1-a)}\]

      ReplyCancel
  5. khan
    1 year ago

    2^(2logcăn(2)(5)+log(1/2)(9)) tính cái ạ

    ReplyCancel
    • 1 year ago

      Câu hỏi của em không thuộc phạm vi vấn đề của bài viết. Em hoàn toàn có thể làm được nó, em tham khảo:

      \[M=2\log_{\sqrt{2}}{5}+\log_{\frac{1}{2}}{9}=2\log_{2^{\frac{1}{2}}}{5}+\log_{2^{-1}}{9}\]
      \[=4\log_{2}{5}-\log_{2}{9}=\log_{2}{5^4}-\log_{2}{9}\]
      \[=\log_{2}{\frac{625}{9}}\]

      Do đó:

      \[2^M=\frac{625}{9}\]

      ReplyCancel

Trả lời

Thapsang.vn

Chào bạn, tôi lập ra trang web này để thỏa mãn sở thích ghi chép, đồng thời chia sẻ những thông tin, kiến thức bổ ích mà tôi biết về dạy và học Toán THPT, văn hóa, giáo dục và công nghệ. Tôi hi vọng bài viết này có ích cho bạn và mong nhận được nhiều phản hồi của bạn. Cảm ơn bạn đã đọc bài viết!

5 years ago 7 Comments Làm toán, , , 1,120